정규분포란?
정규분포(Normal Distribution)는 가우시안 분포(Gaussian Distribution)라고도 알려져 있는데요, 통계학에서의 검정이나 추정, 모델 작성 등 다양한 측면에서 활용되는 연속형 확률분포(Continuous Probability Distribution) 입니다. 데이터 대부분의 값이 가운데에 모여 있고, 중앙에서 멀어질수록 점점 가늘어지는 종형모양으로, 치우침(왜곡 - skewed) 없이 대칭적으로 분포합니다.
정규분포를 구성하는 변수(parameters)로는 평균(mu)과 표준편차(sigma)가 있습니다. 즉, 평균과 표준편차가 달라지면 그래프의 모양도 달라진다는 뜻이 됩니다.
정규 분포(Probability Density Fucntion)를 식으로 나타내면 아래 식이 됩니다. 식을 외우기 보다는 일단 우리가 설명한 변수 μ, σ 값이 변하면 f(x)값도 변하겠구나, 정도만 확인하고 넘어가면 되겠습니다.
f(x)=1√2πσ2exp[−(x−μ)22σ2]
확률 분포이니, 정규 분포 종형의 곡선 아래 전체 면적은 1 이라는 것을 알 수 있습니다. 정규 분포의 x축 값 이상/이하일 확률 등을 정규 분포 곡선 아래 면적을 구하는 것입니다.
아래 그래프는 평균 75, 표준편차가 3인 정규분포를 나타냅니다.

정규분포의 특징
가로축은 관측 데이터(확률 변수)를, 세로축은 그 값이 발생할 확률(확률 밀도)을 나타냅니다. 정규분포의 특성을 정리해보면 다음과 같습니다:
- 좌우 대칭
- 평균에서 관측 데이터가 발생할 확률이 가장 크다.
- 평균과 중간값이 같고, 모두 중앙에 위치한다.
- 평균에서 멀어질수록 발생할 확률은 작아진다.
- 정규분포는 평균과 표준 편차의 두 가지 값으로 설명할 수 있다.
정규분포의 모양은 어떻게 정해질까?
앞에서 잠시 언급했지만, 그래프의 모양은 평균(μ)과 표준 편차(σ)로 결정됩니다. 평균값은 정규 분포의 중심 위치를 결정하고, 표준편차는 정규분포의 좌우 퍼짐 정도를 결정합니다.


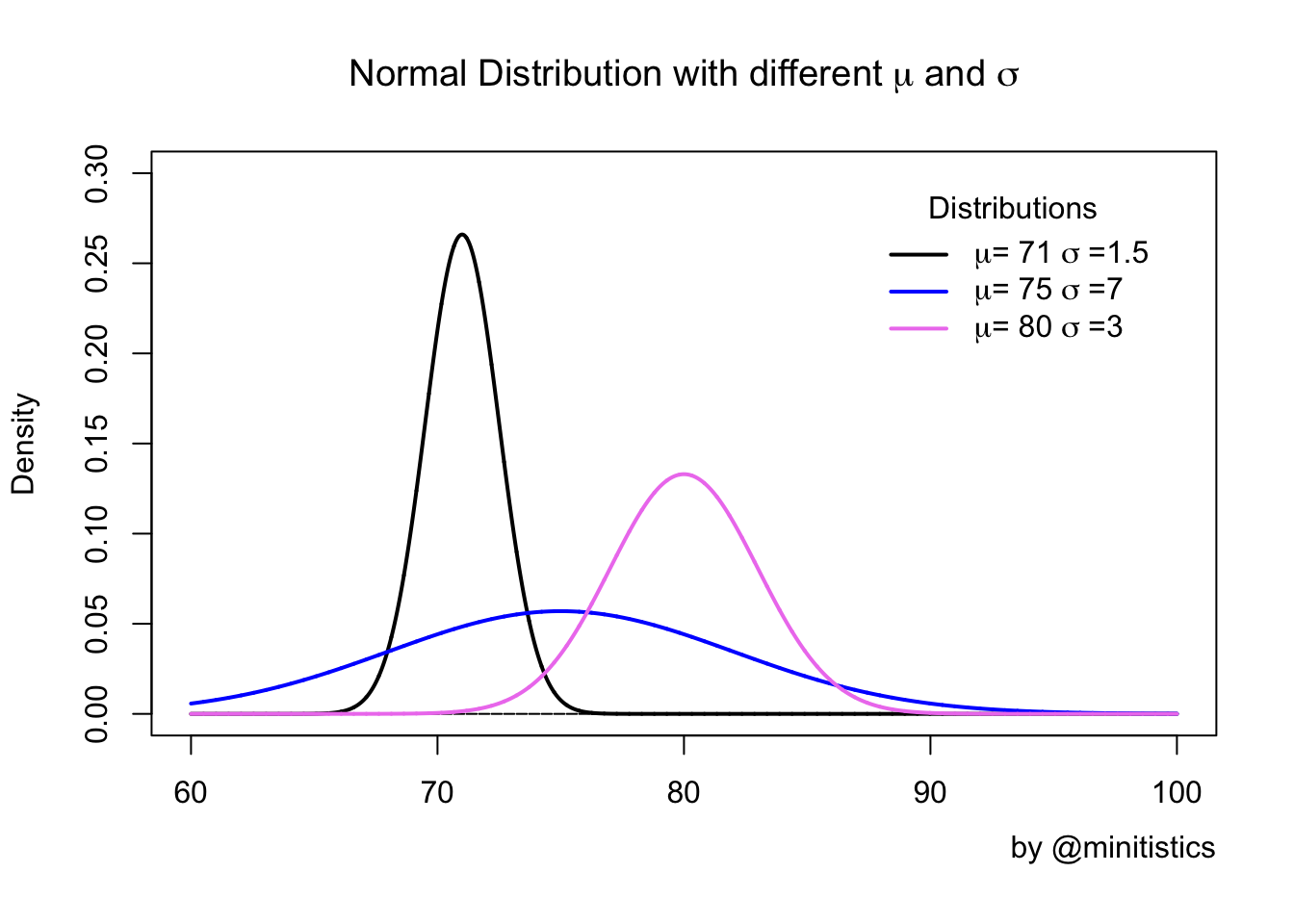
평균값이 높을수록 분포의 중앙값이 우측으로, 낮을수록 좌측으로 이동하며, 표준편차가 높을 수록 퍼짐이 큰 것을 볼 수 있습니다.
정규분포는 왜 중요할까?
왜 통계학을 배우는 데 정규 분포가 중요할까요? 그 이유는 정규 분포를 따르는 자연 현상이나 사회 현상이 많기 때문입니다. 정규 분포의 특성을 이해한다는 것은 표본 집단을 통해 모집단에 대해 추정할 수 있음을 의미합니다. 모집단을 이해하기 위해 모집단 전체를 일일이 조사하는 데에는 시간과 비용이 많이 드는데, 보다 효율적인 방안으로 표본 집단을 통해 모집단을 이해할 수 있는 것이죠.
“모집단의 분포에 관계없이 모집단에서 추출된 표본의 수가 충분히 많을 경우 표본 평균의 분포는 정규 분포에 따른다”라는 성질을 중심극한정리(CLT, Central Limit Theorm),라고 합니다. 이 특성이 존재하기 때문에 수많은 통계 기법은 데이터가 정규 분포를 따르는 것으로 가정합니다.
정규분포에서 알 수 있는 정보는 무엇일까?
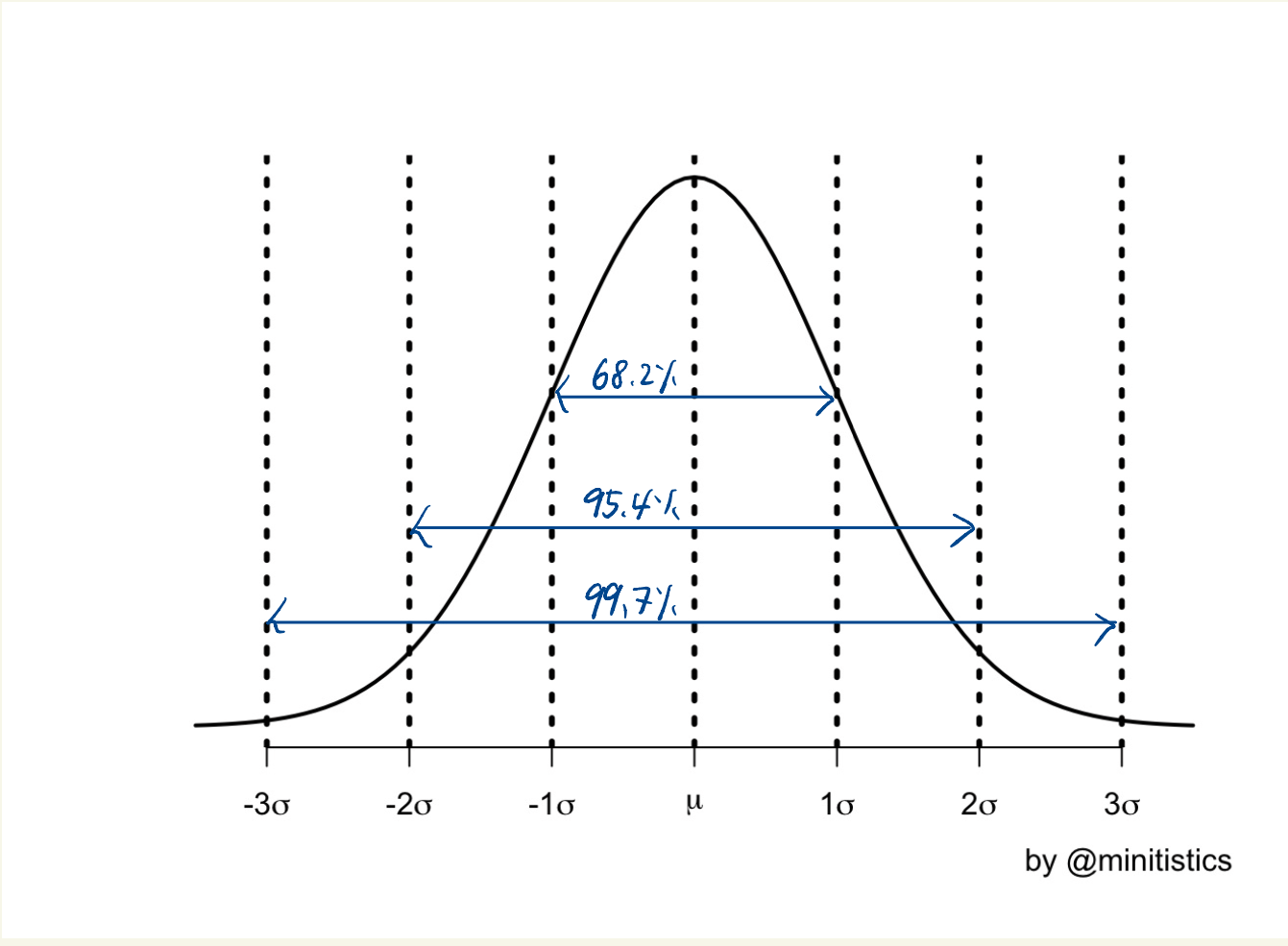
그렇다면 이 정규분포를 통해 어떤 정보를 알 수 있을까요? 평균과 표준 편차를 알면 그 범위에 어느 정도의 관측 데이터가 포함되어 있는지를 알 수 있습니다. 기본 정규분포의 그래프를 나타내보자면 평균을 중심으로 1 표준편차, 2 표준편차, 3 표준편차로 나눌 수 있는데요, 이 그래프의 해석은 아래와 같습니다.
- 데이터 값이 68%의 확률로 평균±표준편차의 범위 내에 존재한다. 즉, 68%의 값이 평균에서 1 표준 편차 내에 있다.
- 데이터 값이 95%의 확률로 평균±2*표준편차의 범위 내에 존재한다. 즉, 95%의 값이 평균에서 2 표준 편차 내에 있다.
- 데이터 값이 99%의 확률로 평균±3*표준편차의 범위 내에 존재한다. 즉, 99%의 값이 평균에서 3 표준 편차 내에 있다.
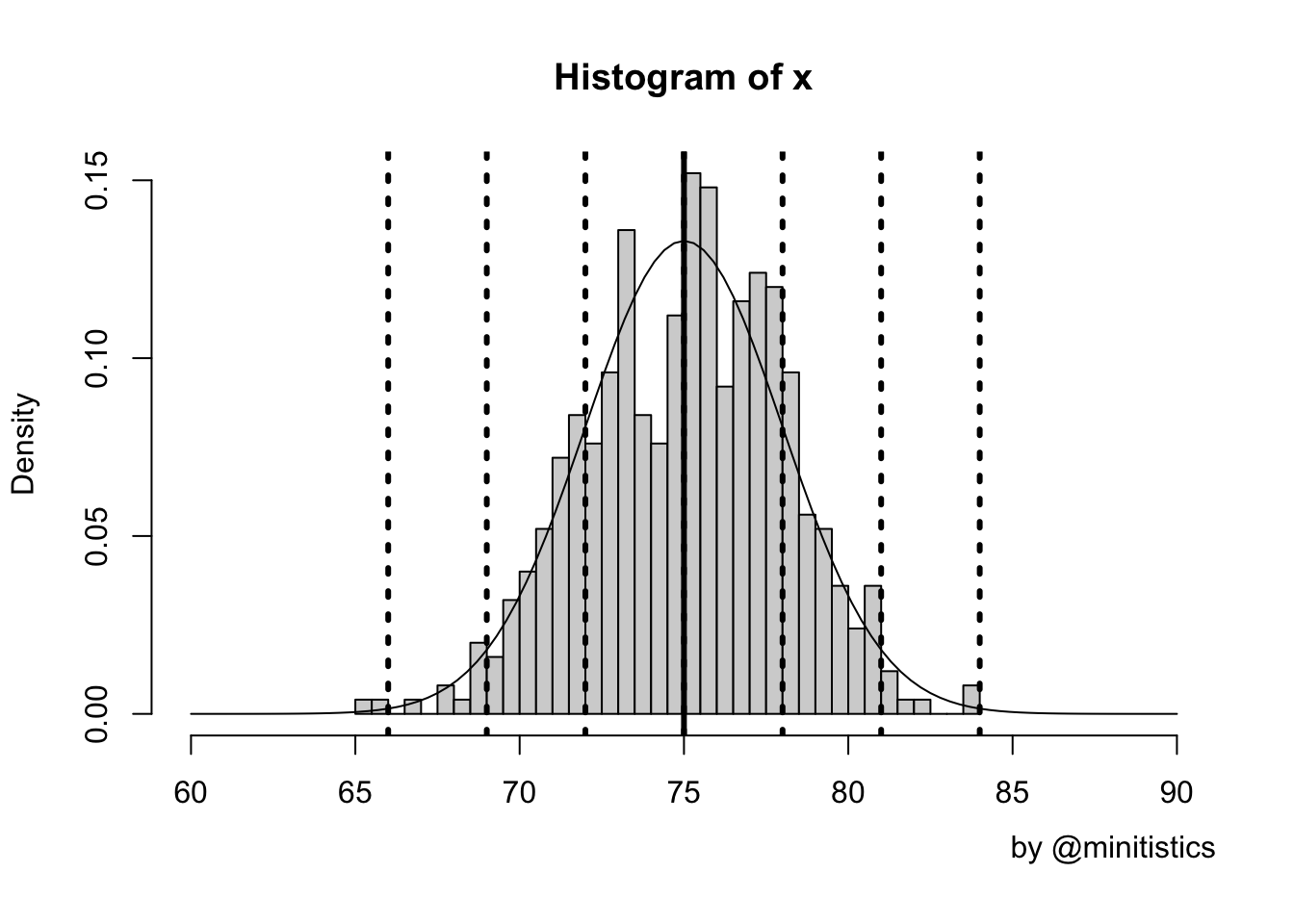
예를 들어, 학생 500명의 한 학교 학생들의 수학 시험 점수 평균이 75, 표준편차를 3이라고 가정하였을 때 다음과 같은 그래프로 나타낼 수 있습니다.
- 500*68% (340명) 정도의 시험 점수가 [72-78]의 범위 내에 존재한다.
- 500*95% (475명) 정도의 시험 점수가 [69-81] 범위 내에 존재한다.
- 500*99% (495명) 정도의 시험 점수가 [66-84] 범위 내에 존재한다.
이와 같은 해석은 후에 통계의 본질인 표본(샘플)을 이용하여 모집단을 추론하는 과정에서 매우 유용하게 사용됩니다. 지금 설명하는 정규분포의 해석은 아주 기초중의 기초이니, μ와 σ가 정규분포에서 어떻게 자리하고 쓰이는지 잘 기억하고 가시길 바랍니다.
+ 정규분포를 계산하기 쉽도록 변환하는 과정을 표준화(Normalise, Standardise) 한다고 하는데요, 이에 대한 포스팅은 표준화 및 표준 정규 분포(Standard Normal Distribution)를 통해 알아볼 수 있습니다. 결국 이 정규분포도 표준화를 이해하기 위한 첫 걸음이 될거에요!
'호주 데이터 분석가 > Stats101' 카테고리의 다른 글
| 귀무가설, 대립가설 그리고 P-hacking (0) | 2023.04.07 |
|---|---|
| m&m 초콜릿으로 P-value 쉽게 이해하기 (0) | 2023.04.06 |
| 표준화 및 표준 정규 분포(Standard Normal Distribution) (0) | 2023.04.04 |
| Box Plot과 Histogram을 이용한 데이터 비대칭 분별 (0) | 2023.04.03 |
| 평균값(Mean), 중앙값(Median), 최빈값(Mode) (0) | 2023.04.02 |




댓글