앞서 일원 분산분석에서 체중감량 프로그램 A, B, C 의 모분산 평균 차이를 비교하여 어느 프로그램이 통계적으로 유의한가를 찾아보는 검정 과정을 R로 함께 풀어보았는데요, 오늘은 잠시 설명했던 이원 분산분석으로 들어가보겠습니다.
2023.04.23 - [Stats101] - 일원 분산분석 (One-way ANOVA)
일원 분산분석 (One-way ANOVA)
t검정의 종류를 정리하면서, 한 그룹(데이터셋 하나)을 그의 기댓값과 비교하거나, 두 그룹의 평균 차이(서로 다른 두 그룹, 혹은 동인한 그룹에서 변화가 있는 경우)가 통계적으로 유의한지를
minitistics.tistory.com
1. One-way Anova(일원 분산분석): 독립 변수가 하나인 경우 (체중감량 프로그램 혹은 성별)
2. Two-way Anova(이원 분산분석): 독립 변수가 둘인 경우 (체중감량 프로그램 + 성별)
이원 분산분석은, 독립 변수가 둘인 경우로 일원 분산분석에서 사용하였던 예시인, 체중감량 프로그램 + 성별이 체중감량에 얼마나 영향을 미치는지, 그리고 그 결과가 통계적으로 유의한지 알아보겠습니다.
1. Exploratory analysis
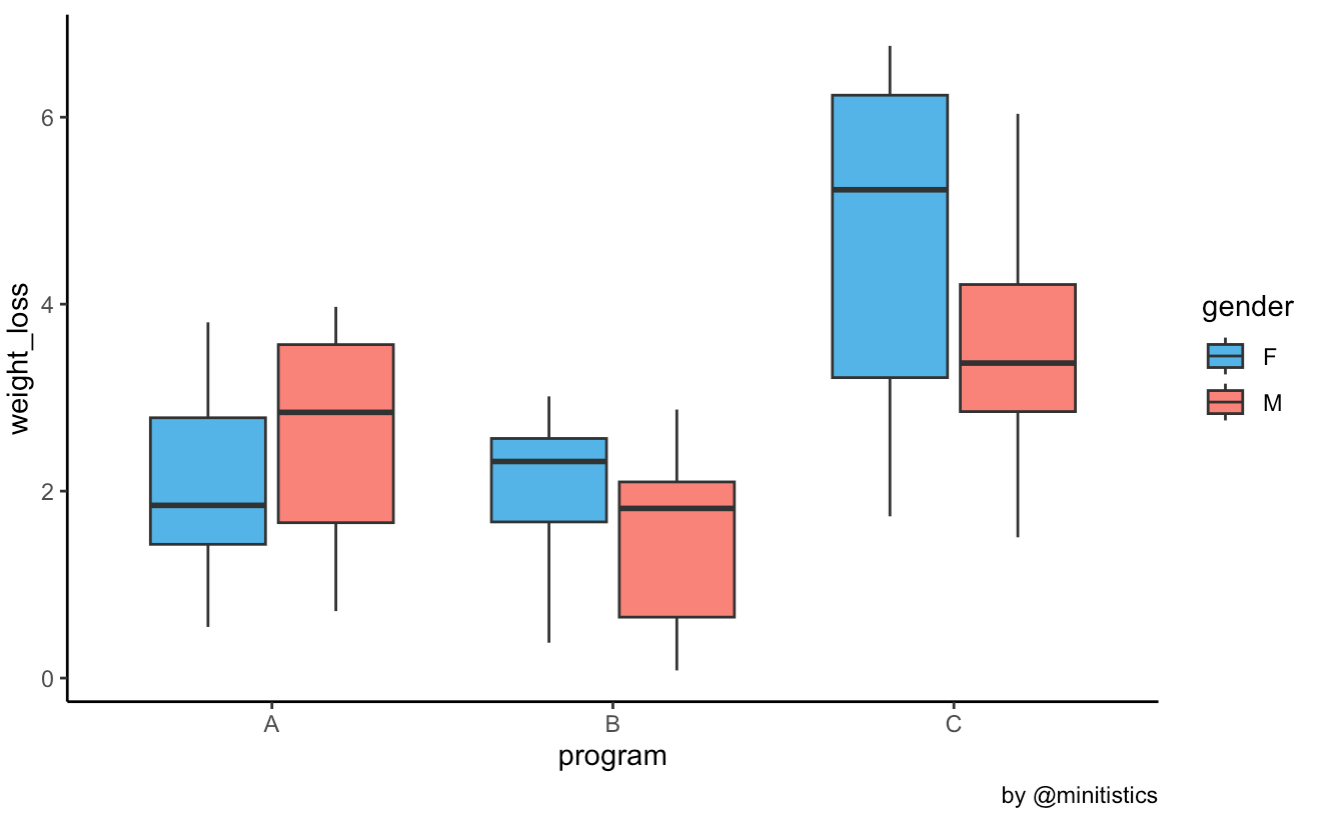
어느 검정에서든 간단한 탐색적 자료분석은 필수입니다. A, B, C 체중감량 프로그램과 성별에 따른 체중변화의 평균과 표준편차, 그리고 이의 분포를 나타내주는 BoxPlot 으로 큰 그림을 먼저 이해합니다. 대체적으로 C 프로그램과, 여성(F-Female)의 체중감량 효과가 크다는 것을 알 수 있습니다.

2. Analysis of Variance (ANOVA): F-test
이원 분산분석 중 우리가 시도해볼 건 additive 모델과, interation 모델입니다.
Additive 모델은 쉽게 말해 산술 합계인 통계 모델로 독립변수의 산술 합계가 종속변수와 같음을 나타냅니다. 즉, 체중감량에 대한 성별과 체중 프로그램의 영향이 독립적으로, 서로 의존하지 않는다는 뜻이 됩니다. (체중감량 = 성별 + 프로그램)
반대로 Interaction 모델은 두 독립변수가 서로 영향을 주며 종속변수를 구성한다는 뜻인데요, 예를들면 체중 감량의 효과에 대한 체중 프로그램의 효과는 성별에 따라 달라진다, 혹은 체중 감량에 영향을 미치는 성별의 효과는 프로그램에 따라 달라진다 정도로 해석할 수 있습니다. ( 체중감량 = 성별 * 프로그램)
이 두 모델을 R에서 시행해본 결과는 다음과 같습니다.
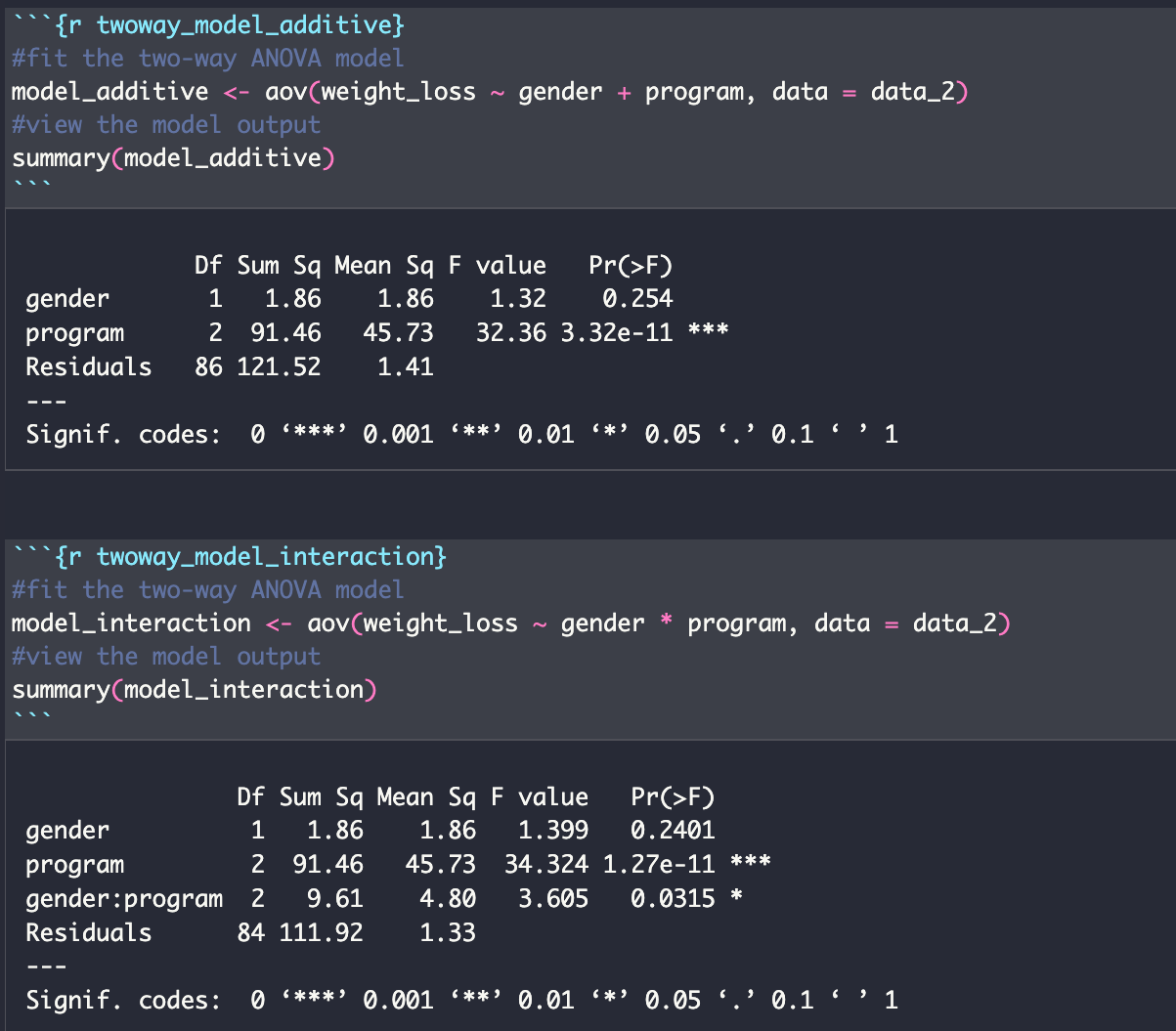
일원 분산분석에서는 잔차의 제곱합(Sum sq)이 125.46 였는데, 이원 분산분석에서 잔차의 제곱합이 감소한 것을 보아, 모델이 개선되었다고 볼 수 있습니다. 또한 Interaction 모델에서는 프로그램 뿐만 아니라, 프로그램과 성별의 영향이 유의할 수도 있다는 해석을 가져다 줍니다.
3. 모델비교
이제 일원 분산분석까지 합하여 세 가지 ANOVA 모델이 있는데요, 이 중 어떤 모델을 선택하여 사용하는 것이 가장 적합한지 결정해야 합니다.
모델의 적합도를 알아보는 여러가지 테스트 중, 우리는 여기서 AIC(Akaike information criterion)를 사용할텐데요. AIC는 기본적으로 우리가 모델에서 사용하는 변수에 따라 설명되는 모델 변동성의 균형을 맞추어 정보의 값을 계산합니다. 언젠가 AIC에 대해 따로 설명을 해볼 것을 리스트에 넣어보며, 일단 지금은 AIC가 가장 낮은 값일 때, 더 많은 정보가 설명된다고 이해하면 됩니다.
다음은 우리가 시험한 세 가지 모델 (일원 분산분석, 이원 분산분석(Additive), 이원 분산분석(Interaction))에 대한 AIC 출력값입니다.
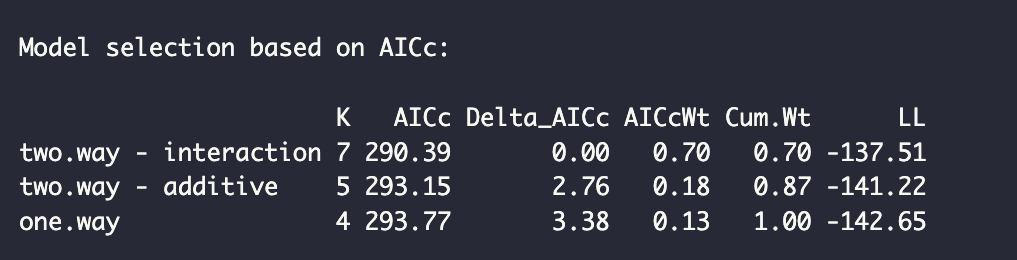
이원 분산분석(Interaction)의 모델의 AIC 값이 290.39로 가장 낮고, AIC 가중치(AIC weight)가 70%로 가장 높습니다. AIC 가중치 비율은 이 모델이 종속 변수의 전체 변동 중 70%정도를 설명한다는 뜻입니다.
그렇다면 최종 선택 모델은 이원 분산분석(상호작용)이 될텐데, 이 모델에서 우리는 성별과 체중 감량 프로그램이 체중 감량에 미치는 영향 사이에는 통계적으로 유의미한 상호작용이 있다는 것을 확인할 수 있습니다(F(2, 84) = 3.605, p = 0.0315).
이원 분산분석의 Interaction(상호작용) 모델을 최종 모델로 선정하기 전, 이 모델의 가정을 점검 합니다.
4. Assumption Check
이쯤되면 이제 우리가 검정해야 할 세 가지 가정이 무엇인지 알 수 있겠죠?
1. 독립성
2. 정규성
3. 등분산성
2023.04.21 - [Stats101] - t 검정의 종류와 방법
t 검정의 종류와 방법
t 테스트는 주로 두 그룹의 평균을 비교하는 데 사용되는 통계 검정입니다. 두 그룹이 서로 다른지 여부를 결정하기 위해 가설 검정에 자주 사용되는데, 언제, 어떤 유형의 t-test를 사용는지 알아
minitistics.tistory.com
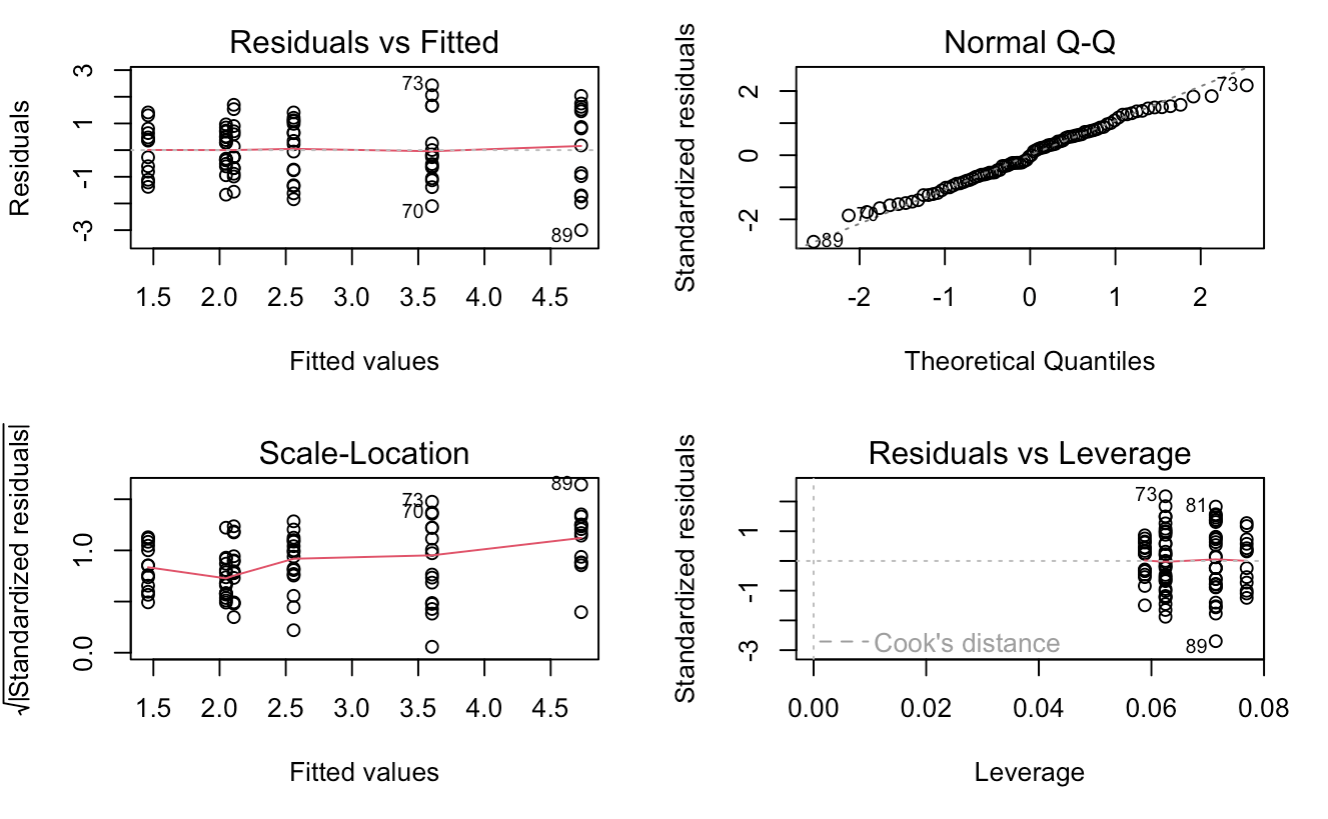
이에 대한 각 뜻과 차트를 보는 방법을 일원 분산분석에서 다루었으니 여기서는 결과 plots만 확인 차 보여드리고 넘어가겠습니다. 결론은 세 가지 가정을 모두 만족하므로, 이원 분산분석(상호작용) 모델로 각 구성의 영향을 파악하는 사후 검정을 해보도록 하겠습니다.
5. 사후검정
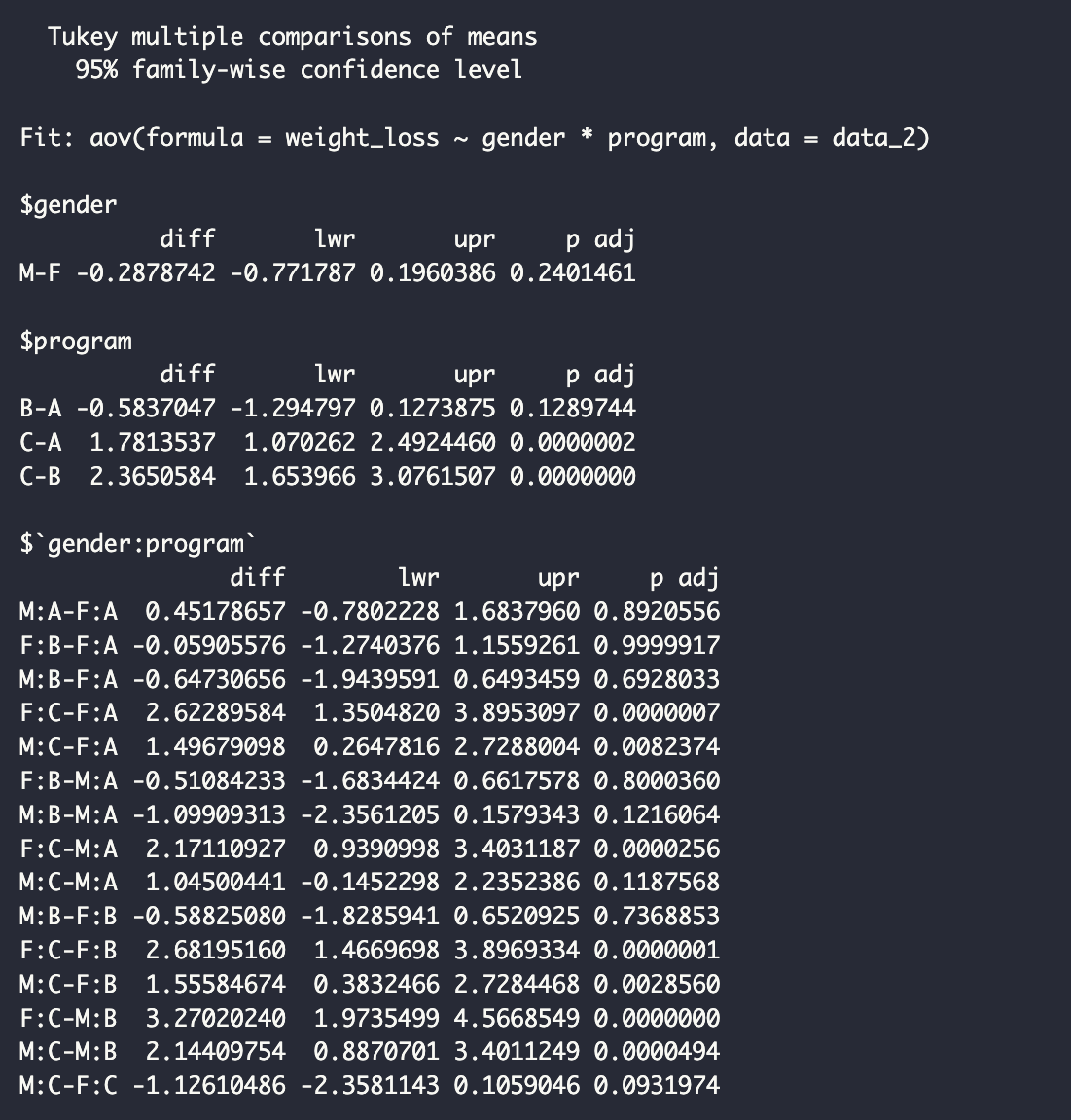
앞서 하였던 Tukey HSD(Tukey Honest Significant Differences)를 상호작용 모델에 사용하였는데요, 각각의 결과에서 p-값은 각 그룹 간에 통계적으로 유의한 차이가 있는지 여부를 나타냅니다. 성별별로, 감량 프로그램을 살펴보면, 남성의 경우 체중 감량 프로그램 C는 B(p < .0001)에 비해 체중 감량 폭이 컸으며, 여성의 경우, 체중 감량 프로그램 C는 B(p < .0001)와 A(p < .0001) 와 비교하여 비슷하게 높은 수준으로 체중 감량이 이루어졌습니다.
가장 유의한 결과를 찾아보자면, F:C-M:B로, 여성이 C프로그램을 사용하였을 때, 남성 B 프로그램에 비해 매우 높은 체중 감량 효과(평균적 차이 3.27kg, p-value <.0001)를 가져온다가 될 수 있습니다. 여성에게 체중감량을 위한 프로그램으로는 C가 제격이겠구나, 하는 결과를 얻은 셈이 되는거죠.
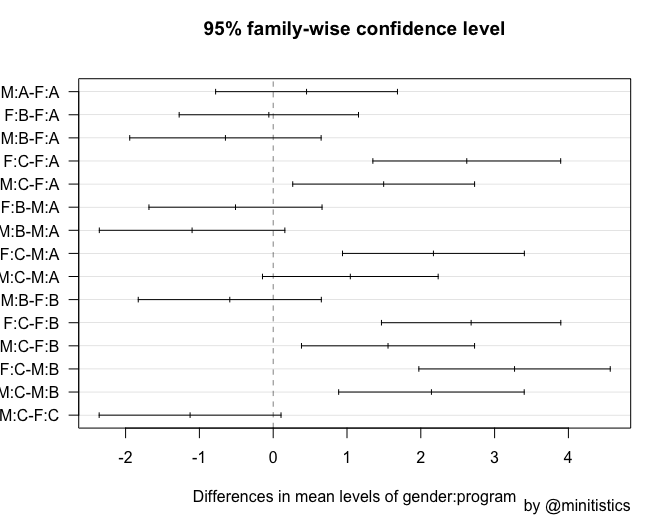
아래는 R 사후검정 결과 중 95% 신뢰 구간을 시각화 하였는데요, 위의 해석과 같이 F:C-M:B가 가장 유의한 차이를 나타낸다는 것을 확인할 수 있습니다.
'Stats101' 카테고리의 다른 글
| 카이제곱 적합도 검정(feat. m&m) - Goodness of fit test (2) | 2023.04.28 |
|---|---|
| AIC(Akaike Information Criterion) (0) | 2023.04.25 |
| 일원 분산분석 (One-way ANOVA) (0) | 2023.04.23 |
| t 검정의 종류와 방법 (0) | 2023.04.21 |
| t-분포(t-Distribution) (0) | 2023.04.19 |




댓글