t 테스트는 주로 두 그룹의 평균을 비교하는 데 사용되는 통계 검정입니다. 두 그룹이 서로 다른지 여부를 결정하기 위해 가설 검정에 자주 사용되는데, 언제, 어떤 유형의 t-test를 사용는지 알아보겠습니다.
2023.04.19 - [분류 전체보기] - t-분포(t-Distribution)
t-분포(t-Distribution)
t-분포란? t-분포 Student's t-distribution 이라고도 알려져있는데요, 모집단의 분산을 알 수 없는 더 작은 표본 크기에 사용되는 정규 분포 유형입니다. t분포를 그려보면 정규분포와 같이 종 모양을
minitistics.tistory.com
t-test를 이해하기 위해 매뉴얼로 계산한다고 하면 z-test에서 정규분포표를 사용하였듯 t-table을 사용할 텐데요. t-table 을 사용하여 t-score를 구하기 앞서 정해야 할 목록이 있습니다.
- 유의 수준(1%, 5%, 10%)
- 자유도(DF)
- 단측, 양측 중 어느 가설 검정을 할 것인가.
아래 표를 보면, 이 세 가지를 알았을 때 t-table에서 t-score를 구할 수 있음을 알 수 있습니다. 이번 포스팅에서는 이 t-test를 직접 계산하는 법과, R로 수행하는 법을 배워볼 거예요.

2023.04.04 - [Stats101] - 표준화 및 표준 정규 분포(Standard Normal Distribution)
표준화 및 표준 정규 분포(Standard Normal Distribution)
정규분포(Normal Distribution)에서 잠시 언급하였듯, 정규 분포를 따르는 자연 현상이나 사회 현상은 무궁무진합니다. 그만큼 정규분포를 구성하는 평균과 분산이 다양하기 때문에, 세상의 모든 정
minitistics.tistory.com
언제, 어떤 유형의 t 테스트를 사용해야 할까?
1. 단일표본 t-test (one-sample t-test)
단일 표본의 평균에 대한 가설 검정, 즉 표준값과 비교되는 그룹이 하나 있는 경우에 사용합니다. 예를 들어 교실의 시험 점수를 전국 평균 시험 점수와 비교하는 거에요.
평균적으로 학생들이 시험에서 300점 이상을 득점하는지 확인하고 싶다고 가정해 보겠습니다. 전체 학생 점수의 분산(또는 표준편차)에 대한 정보가 없기 때문에 점수가 있는 10명의 학생 데이터를 무작위로 수집하고 유의수준($\alpha$)을 5%로 선택합니다. 검정을 시작하기 전, 귀무가설, 대립가설을 설정하는데, 우리가 확인하고 싶은 사항을 대립가설로 세웁니다. 우리가 확인하고 싶은 바를 뒷받침할 증거가 충분히 있는지를 테스트하는 거죠.
$$귀무가설(H_{0}): \mu <= 300$$
$$대립가설(H_{1}): \mu > 300$$
표본 = [270, 290, 305, 320, 280, 295, 380, 320, 280, 370]
- 모평균 = 300
- 표본 평균 = 311
- 표본 표준편차 = 37.6
- 표본 크기 = 10
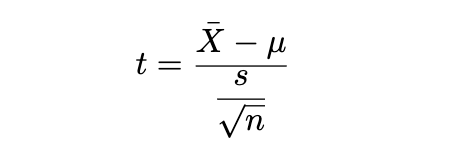
이 식에 따라 t-score = (311-300)/(37.6/$\sqrt{10}$) = 0.925
Critical value(임계값) = 1.833 ( 위의 t-table에서 한 번 찾아보시는 걸 추천합니다. 자유도(df) = 9, 유의수준(⍺) =0.05, one-tail) 을 확인한 후, t-score와 임계갑을 비교합니다(t-score < Critical value). t-score 절댓값이 임계값보다 크면 귀무가설을 기각하고, 작으면 귀무가설을 기각할 수 없으므로 우리는 여기서 평균값이 300보다 작거나 같다는 귀무가설을 기각할 충분한 근거가 없음을 알 수 있습니다. p-value 를 구하여 유의 수준과 비교해 보겠습니다.

p-value는 0.05보다 크므로 귀무가설을 기각하지 못합니다. 즉, 학생들의 시험 평균이 300을 넘는다고 할 수 있는 증거가 충분하지 않습니다. 귀무가설, 대립가설과 p-value 해석에 대한 포스팅은 아래를 참조해주세요.
2023.04.07 - [Stats101] - 귀무가설, 대립가설 그리고 P-hacking
귀무가설, 대립가설 그리고 P-hacking
왜 귀무가설을 통해 대립가설을 증명할까 앞서 m&m 초콜릿으로 P-value 쉽게 이해하기 에서 P-value를 통해 [귀무가설을 기각한다.] 라고 했는데요, 왜 [대립가설을 받아들인다.] 라고 하지 않고, 꼭
minitistics.tistory.com
2023.04.06 - [Stats101] - m&m 초콜릿으로 P-value 쉽게 이해하기
m&m 초콜릿으로 P-value 쉽게 이해하기
P-value의 P는 [Probability]에서 나온 단어인데요. 그렇다면 "무슨"확률을 뜻하는 걸까요? P-value는 귀무가설($H_0$, null hypothesis)이 사실일 때, 데이터에서 관찰된 값, 혹은 그 이상의 결과를 관찰할 확률
minitistics.tistory.com
2. 독립표본 t-test(two-sample t-test)
서로 다른 두 독립 표본의 평균 차이에 대한 가설검정으로 두 데이터 그룹의 평균을 비교합니다. (서로 다른 두 학급의 평균 시험 점수를 비교). two-sample t-test의 t-score는 다음과 같이 구합니다.
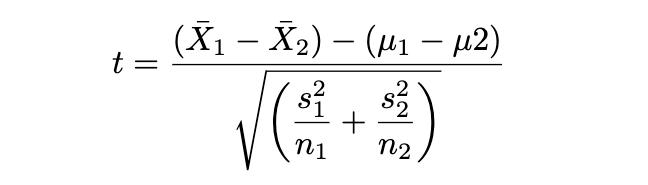
단일 검정은 거의 매뉴얼로 하였으니, 다음 독립표본 t검정은 R을 사용해 보겠습니다.
[여성의 평균 몸무게가 남성의 평균 몸무게와 같은가]를 대답하기 위해 여성 10명 남성 10명을 표본으로 뽑아 t-test를 실행합니다.
귀무가설: $ \mu_{w} = \mu_{m}$
대립가설: $\mu_{w} <> \mu_{m}$
여성과 남성의 몸무게의 평균과 표준편차는 다음과 같습니다.

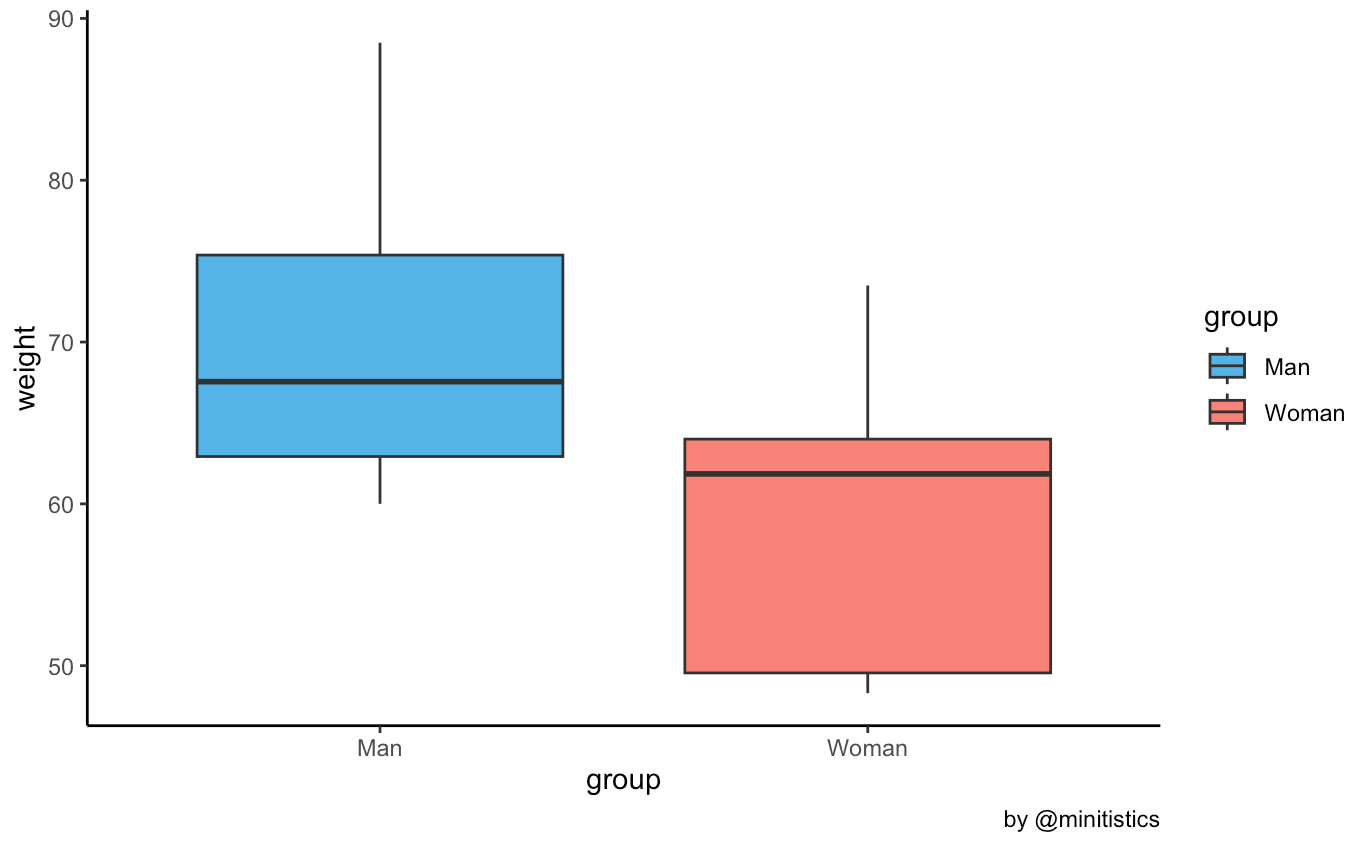
two-sample t-test 를 적용하기 전에 표본이 t-test를 하기 적합한지 가정을 검사해야 하는데요, 여기에 세 가지가 있습니다. (이 세가지 개념은 앞으로 종종 등장할 예정이니 잘 기억하도록 해보아요.)
(1) 독립성 (independency): 남성과 여성이라는 서로 다른 그룹에서 표본을 추출하였으므로, 두 그룹은 서로 독립적이라고 할 수 있습니다.
(2) 정규성(normality) : Shapiro-Wilk normality test를 통해 검사합니다.
귀무가설: 데이터가 정규분포를 따른다.
대립가설: 데이터가 정규분포를 따르지 않는다.
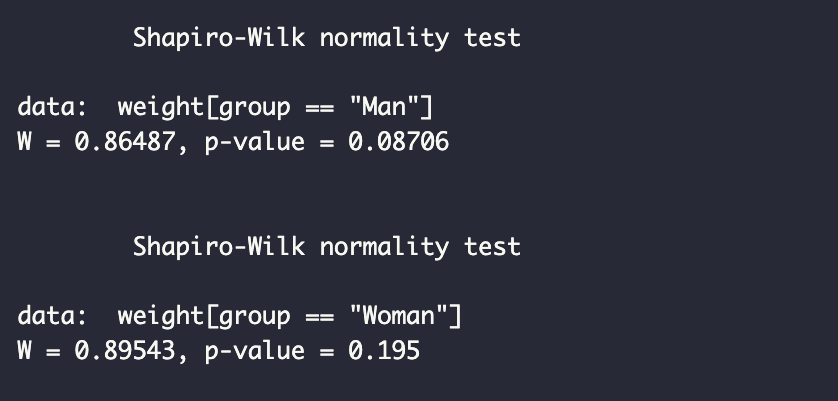
남성 그룹과 여성 그룹에 Shapiro-Wilk 검정을 한 결과, 두 그룹 모두 p-value가 유의수준(0.05)보다 높아 귀무가설을 기각할 증거가 충분하지 않다고 볼 수 있습니다. 즉, 두 그룹 모두 정규분포를 따른다고 가정할 수 있는 거죠. (만약 데이터가 정규 분포를 따르지 않는 경우라면, two-sample Wilcoxon rank test를 사용합니다.)
(3) 등분산성(eov - equal of variance test)
등분산성에서는 두 모집단이 각각 같은 분산에서 왔느냐는 질문을 검정합니다. 등부산성이 성립할 때 t-test를 사용할 수 있습니다.
귀무가설: 두 모집단의 분산이 같다.
대립가설: 두 모집단의 분산이 같지 않다.

F-테스트의 p-값은 p = 0.6793입니다. 결론적으로 두 데이터 세트의 분산 간에는 큰 차이가 없다고 받아들일 수 있습니다. 따라서 우리는 두 분산이 동일하다고 가정할 수 있습니다.
자, 이제 데이터가 모든 가정을 만족하였음을 확인하였으므로, 드디어 t-test를 시행해 봅니다!

- t = 2.7031: t는 t-test 결과로 t-score와 같습니다.
- df = 18: 자유도는 one-sample에서는 (n-1)이었고, two-sample에서는 (n1+n2-2)로 20-2=18 이 됩니다.
- p-value = 0.01455
- 95% confidence interval: 95% 신뢰구간으로, 두 모집단 평균의 차이가 [2.63, 20.97], 즉 두 모집단의 평균 체중 차이가 95% 확률로 2.63kg와 20.97kg 사이에 있다고 해석할 수 있습니다.
- sample estimates: 표본의 평균을 나타내며, 제일 처음 exploratory analysis차원에서 했던 박스를 보시면 그곳의 평균값과 같음을 알 수 있습니다.
자! 그럼 결론 해석으로 들어가겠습니다. t-test의 p-value는 0.01455로, 유의 수준 5%(0.05) 보다 작습니다. 즉, 여성과 남성의 평균 체중이 통계적으로 유의하게 다르다는 결론을 내릴 수 있습니다.
3. 대응표본 t-test(paired t-test)
동일 집단의 변화를 나타내는 평균의 차이에 대한 가설검정입니다. 이 테스트는 동일한 한 그룹에 시험을 가한 후 지켜보며 평균의 변화를 비교합니다(약 투여 전후의 몸무게 변화).

m: 두 그룹 평균 차이
s: 두 그룹 차이의 표준편차
n: 몇 쌍인가
귀무가설: m = 0
대립가설: m <>0
대응표본 테스트로는 R 데이터패키지(package = "datarium")에 이미 있는 실험쥐 before & after 결과를 사용하였습니다.


독립표본 two-samle test에서 추정한 세 가지 테스트를 여기서도 하는데요:
(1) 두 그룹의 데이터가 서로 대응하는가?
즉, 한 쌍을 이루는가(paired)를 체크하는데, before와 after로 같은 집단을 테스트하였으므로 이 가정은 성립합니다.
(2) 표본이 큰가? (30 이상인가?)
n < 30으로 표본이 작다고 할 수 있습니다. 샘플 크기가 충분히 크지 않기 때문에(여기서는 10) 쌍의 차이가 정규 분포를 따르는지 확인해야 합니다.
(3) 정규성(normality) : Shapiro-Wilk normality test를 통해 검사합니다.
귀무가설: 데이터가 정규분포를 따른다.
대립가설: 데이터가 정규분포를 따르지 않는다.

지금까지 잘 따라오셨다면, 이 결과의 의미를 아실거에요. 바로 before와 after의 차이가 정규분포를 따른다고 가정할 수 있다! 이죠. 이제 paired t-test를 해보겠습니다.
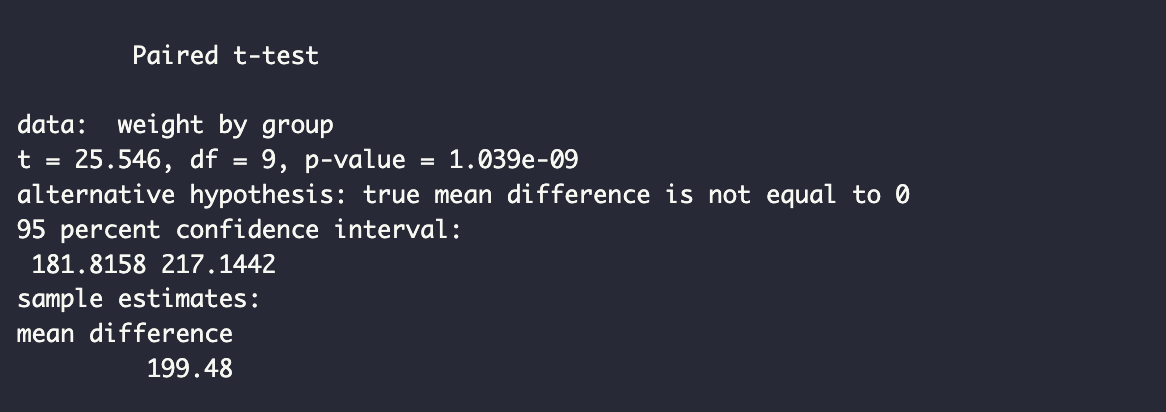
- t = 25.546: t는 t-test결과로 t-score와 같습니다.
- df = 9: 동일 그룹에서 온 표본으로 n-1=9입니다.
- p-value = 1.039e-09
- 95% confidence interval: 95% 신뢰구간으로, before & after 평균의 차이가 [181.8, 217.1], 즉 before & after 평균의 차이가 95% 확률로 181.8와 217.1 사이에 있다고 해석할 수 있습니다.
- sample estimates: 표본의 평균을 나타내며, 제일 처음 exploratory analysis차원에서 했던 박스를 보시면 그곳의 before & after 평균의 차이와 같음을 알 수 있습니다 (400.04-200.56)
대응표본의 예시로 든 t검정의 p-value는 유의 수준 5%보다 작습니다. 귀무가설을 기각함으로써, 약물 투여 전 마우스의 평균 체중이 투여 여 후 평균 체중과 통계적으로 유의하게 다르다는 결론을 내릴 수 있습니다.
'Stats101' 카테고리의 다른 글
| 이원 분산분석(Two-way ANOVA) (0) | 2023.04.24 |
|---|---|
| 일원 분산분석 (One-way ANOVA) (0) | 2023.04.23 |
| t-분포(t-Distribution) (0) | 2023.04.19 |
| Confusion Matrix (0) | 2023.04.17 |
| 표준오차, 표본오차와 신뢰구간 (1) | 2023.04.16 |




댓글