t검정의 종류를 정리하면서, 한 그룹(데이터셋 하나)을 그의 기댓값과 비교하거나, 두 그룹의 평균 차이(서로 다른 두 그룹, 혹은 동인한 그룹에서 변화가 있는 경우)가 통계적으로 유의한지를 위한 가설 검정이라는 것을 배웠습니다. 그런데, 세상에 딱 두그룹만 비교하는 일만 있지 않습니다. 만약에 비교해야할 대상이 두 그룹이 넘어가면 어떤 가설 검정을 사용해야할까요?
2023.04.21 - [Stats101] - t 검정의 종류와 방법
t 검정의 종류와 방법
t 테스트는 주로 두 그룹의 평균을 비교하는 데 사용되는 통계 검정입니다. 두 그룹이 서로 다른지 여부를 결정하기 위해 가설 검정에 자주 사용되는데, 언제, 어떤 유형의 t-test를 사용는지 알아
minitistics.tistory.com
두 그룹 이상의 그룹 평균 간의 차이를 통계적으로 검정하기 위해 분산분석(ANOVA: Analysis of Variance)을 사용합니다. 분산분석은 크게 독립변수의 수에 따라 두가지로 나뉘는데요. 예를들어, A, B, C라는 체중감량 프로그램(범주형 독립변수)에 따른 남녀(범주형 독립변수) 참가자 몸무게 변화(양적 종속변수)에 대해 테스트해보고 싶다고 가정해봅니다.
1. One-way Anova(일원 분산분석): 독립 변수가 하나인 경우 (체중감량 프로그램 혹은 성별)
2. Two-way Anova(이원 분산분석): 독립 변수가 둘인 경우 (체중감량 프로그램 + 성별)
즉, 하나의 독립변수와 그에 대응하는 종속변수라면 일원, 독립변수가 둘이면 이원이 되는 것이죠. 먼저 우리는 A, B, C의 체중감량 효과가 서로 다른지 알아보기로 하겠습니다.
귀무가설: 모든 세 그룹(A, B, C)의 체중변화가 같다.
대립가설: 적어도 한 쌍의 체중변화가 다르다.
그러면 이제 임의로 만든 데이터를 통해 A, B, C 그룹의 체중변화에 대한 테스트를 해보도록 하겠습니다.
1. Exploratory analysis
간단하게 탐색적 자료분석을 먼저 해봅니다. A, B, C 그룹의 평균 체중변화와 표준편차, 그리고 이의 분포를 나타내주는 BoxPlot 으로 각 그룹 데이터의 큰그림을 이해하는데 유용합니다.
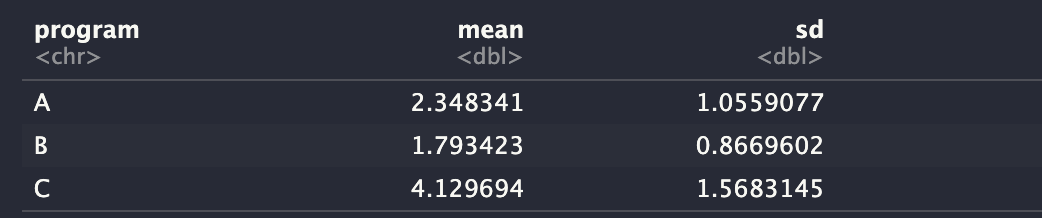

언뜻 봐도 차이는 있는데, 정말 통계적으로 유의한지 이제부터 살펴볼거에요.
2. Analysis of Variance (ANOVA): F-test
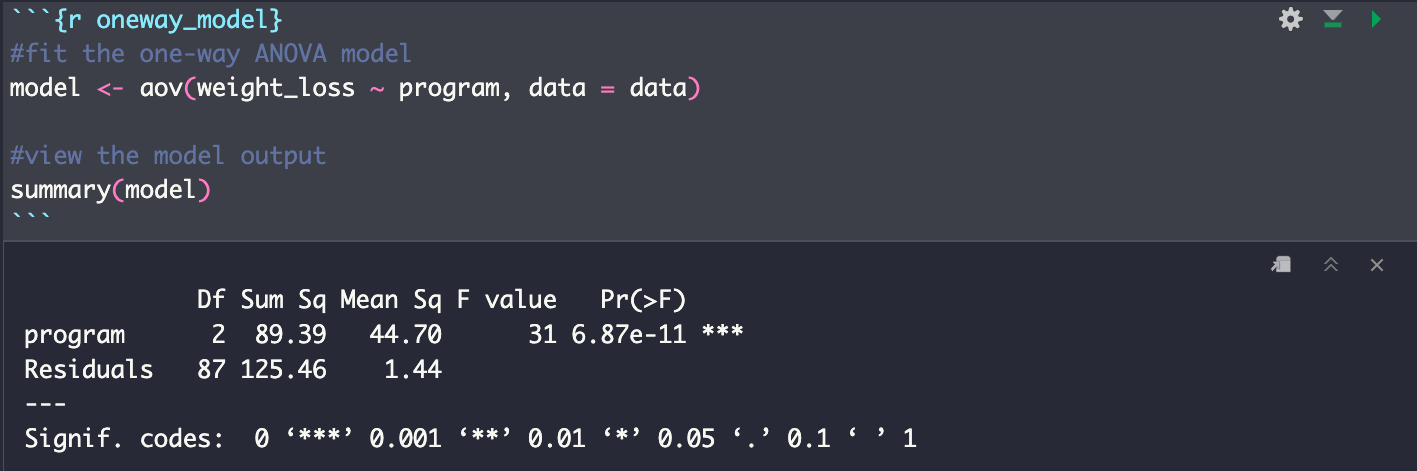
ANOVA를 F-test라고도 하는데요, summary에 보면 F-test를 하기 위한 F-value가 있고, 해당 F값에 해당하는 P-value가 매우 작음을 알 수 있습니다.
F-test는 가설검정 시 F-value를 사용합니다(이전에 우리가 t-test에 t-value(t-score, t값)을 사용했던 것 처럼요). F값은 두 분산의 비율인데요, 식은 다음과 같습니다.
F = 그룹 간 분산(between-groups variance)/그룹 내 분산(within-group variance)
식에서 보는 것과 같이 F-test는 전체 그룹 분산에서 각 그룹 평균의 분산을 비교합니다. 그룹 내 분산이 그룹 간 분산보다 작으면 F 값이 높아지기 때문에 데이터에서 관찰된 차이가 우연이 아니라 실제일 가능성이 더 높아집니다. (즉, 귀무가설을 기각합니다 - 이는 p-value에서 설명했었죠.)
- 자유도(df1): 독립 변수(여기서는 A, B, C 프로그램)에 대한 자유도(독립변수 수에서 1을 빼기: 3-1)
- 자유도(df2): 잔차(residuals)에 대한 자유도(총 표본 수에서 그룹 수 빼기: 90-3).
- Sum Sq: 그룹 평균과 해당 변수에 의해 설명되는 전체 평균 사이의 제곱합(총 변동)을 표시합니다. 프로그램 변수(A, B, C)의 제곱합은 89.39인 반면 잔차의 제곱합은 125.46입니다.
- Mean Sq: 제곱합(Sum Sq)을 자유도로 나누어 계산되는 제곱합의 평균입니다.
- F-value: F 검정의 검정 통계량. 각 독립 변수의 평균 제곱(그룹 간 분산)을 잔차의 평균 제곱(그룹 내 분산)으로 나눈 값입니다. 즉, 44.70/1.44 = 31. F 값이 클수록 귀무가설을 기각할 확률이 높아집니다. (독립 변수와 관련된 변동이 우연히 발생하는 것이 아니라 실제일 가능성이 커진다는 뜻이죠.)
- Pr(>F): F 통계의 p-value입니다. 이는 그룹 평균 간에 차이가 없다는 귀무가설이 참일 경우 검정에서 계산된 F 값이 발생했을 확률입니다.
P-value가 유의 수준 5%보다 작은데 옆에 별표 "***"의 수를 통해 얼만큼 유의한지의 strength를 나타냅니다. 위의 결과로 보면, 우리는 귀무가설을 기각할 증거가 충분히 있다고 해석할 수 있죠. 즉, 세 그룹 중 어느 한 쌍의 그룹 간 몸무게 차이가 매우 유의하다, 라는 결론을 내릴 수 있습니다.
3. Assumption Check
그럼 도대체 어떤 그룹간에 그리 유의한 차이가 있었을까? 궁금해지죠. 그런데 여기서 더 진행하기 전에 결과를 신뢰할 수 있는지, 우리가 t-test에서 했던 것과 같이 모델의 가정이 충족되었는지 확인해야 합니다. 검사해야할 가정이 세 가지 있었는데 기억하시나요?
1. 독립성(independence): 각 그룹의 관측값은 서로 독립적이어야 합니다.
2. 정규성(normallity): 각 독립변수에 따른 종속 변수는 (대략)정규 분포를 따라야 합니다.
3. 등분산성(equal of variance): t-test에서는 등분산성 정도로 하고 넘어갔는데, 이 성질은 Homoscedasticity 라고도 합니다. 각 그룹의 분산이 (대략) 같아야 한다는 가정입니다.
1번 독립성은 테스트의 성격상 우리가 무작위로 남녀를 뽑아 프로그램을 수행한 것이기 때문에 독립성을 충족한다고 할 수 있습니다. 2번 정규성과, 3번 등분상성을 한번에 확인할 수 있는 그래프를 보여드릴게요.
여러가지 Plots이 있지만 이 중 눈여겨 본 것은 빨간 선의 위치와 모양, 그리고 Normal Q-Q plot입니다.
잔차(residuals)의 평균을 나타내는 빨간색 선이 수평에 가깝고, 0 중심에 있다는 것으로 각 그룹의 분산이 일정하다는 것을 알 수 있습니다. 약간의 아웃라이어(데이터 포인트 81, 90) 가 있지만, 크게 영향을 줄 정도가 아니므로 그대로 진행합니다.
Normal Q-Q 역시 완벽한 등분산 모델의 이론적 잔차(점선으로 나타내어진 부분)와 모델의 실제 잔차 사이의 회귀를 표시하므로 기울기가 1에 가까울수록 좋습니다. 우리의 플랏을 보면 거의 직선에 가깝게 따르기 때문에 데이터의 정규성을 증명합니다.

정규성으로는 Shapiro-Wilk test 도 가능합니다.

4. 사후검정
ANOVA는 독립 변수 중 적어도 한 쌍에서 유의한 차이가 발견되는지는 알려 주지만 어느 그룹간의 차이가 중요한지는 알려주지 않습니다. 이때 수행하는 테스트로 Tukey HSD(Tukey Honest Significant Differences)를 사용할 수 있는데요, 결과는 아래와 같습니다.

별표로 보여주지는 않지만, p-value가 유의수준(5%)에 비해 현저히 낮은 그룹을 볼 수 있습니다 (C-A, C-B).
- diff: 두 그룹의 평균 차이
- lwr, upr: 95%에서 신뢰 구간
- p adj: 다중 비교를 위한 조정 후의 p-value.
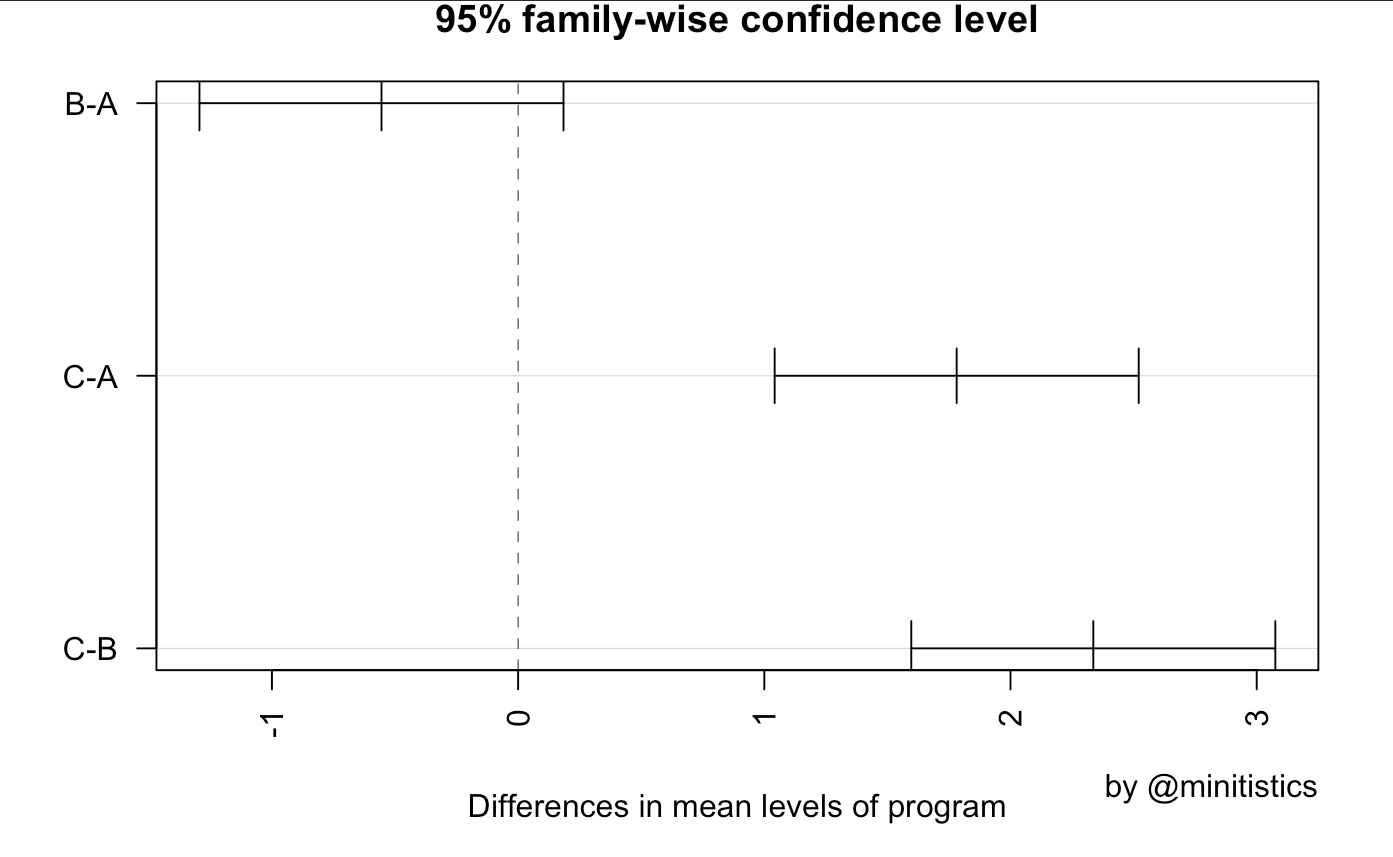
결론은 A, B, C 세가지 체중감량 프로그램 중 C가 통계적으로 유의한 결과를 나타낸다고 할 수 있습니다. 즉, C의 체중감량 프로그램이 다른 프로그램에 비해 몸무게 감소 효과가 크다는 것을 일원 분산분석(One-way ANOVA), F검정을 사용하여 다루어보았습니다.
'Stats101' 카테고리의 다른 글
| AIC(Akaike Information Criterion) (0) | 2023.04.25 |
|---|---|
| 이원 분산분석(Two-way ANOVA) (0) | 2023.04.24 |
| t 검정의 종류와 방법 (0) | 2023.04.21 |
| t-분포(t-Distribution) (0) | 2023.04.19 |
| Confusion Matrix (0) | 2023.04.17 |




댓글