정규분포는 평균과 표준편차에 의해 분포의 모양이 결정됩니다. 여기서 표준편차는 분산의 제곱근으로 데이터의 변동성을 나타내는데요, 변동성이란 데이터가 서로 그리고 분포 중심(mu)에서 얼마나 멀리 떨어져 있는지를 나타냅니다.
2023.04.01 - [Stats101] - 정규 분포(Normal Distribution)
정규 분포(Normal Distribution)
정규분포란? 정규분포(Normal Distribution)는 가우시안 분포(Gaussian Distribution)라고도 알려져 있는데요, 통계학에서의 검정이나 추정, 모델 작성 등 다양한 측면에서 활용되는 연속형 확률분포(Continuou
minitistics.tistory.com
변동성의 정도에 따라 표본 집단(샘플)의 결과를 모집단에 얼마나 잘 일반화할 수 있는지 결정되기 때문에 이는 중요합니다. 낮은 변동성은 표본 집단을 기반으로 모집단에 대한 정보를 더 잘 예측할 수 있음을 의미하고, 변동성이 높다는 것은 값의 일관성이 낮아 예측하기가 더 어렵다는 것을 의미합니다.
변동성이 어떻게 정규분포에 영향을 미치는지 표준편차가 커지면 정규분포의 분포가 납작해지고, 표준편차가 작아지면 정규분포의 모양이 뾰족해지는 아래의 그래프로 확인할 수 있습니다.
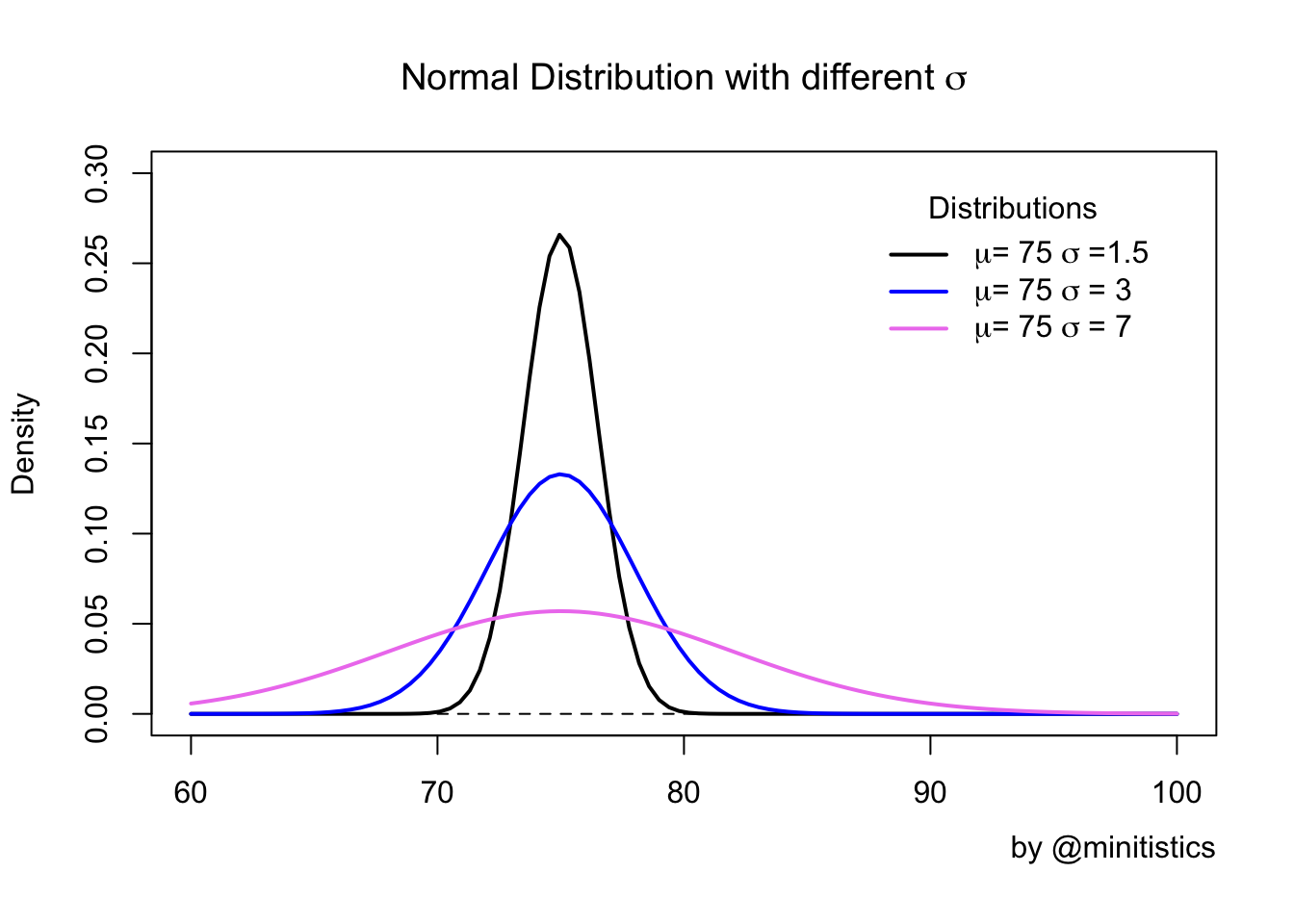
분산은 평균에서 제곱 거리의 평균을 나타내고, 분산의 제곱근인 표준 편차는 평균에서의 평균 거리를 나타내는데요, 경우에 따라서는 이렇게 말로 풀어진 것을 수식으로 나타내면 이해할 때 도움이 되니 써보자면:
모집단(population)의 분산 공식

그리고 표준 편차는 분산의 제곱근으로,

계산을 직접 해보도록 할게요. 학생 10명의 아이큐 검사에 대한 분산과 표준편차를 구해보려고 합니다. 아이큐 결과값은 [95, 107, 103, 86, 97, 115, 93, 106, 99, 120] 입니다. 이 값들의 평균($\mu$)은 102 입니다. 각 데이터 포인터의 평균에서의 거리를 계산하면 아래와 같습니다.
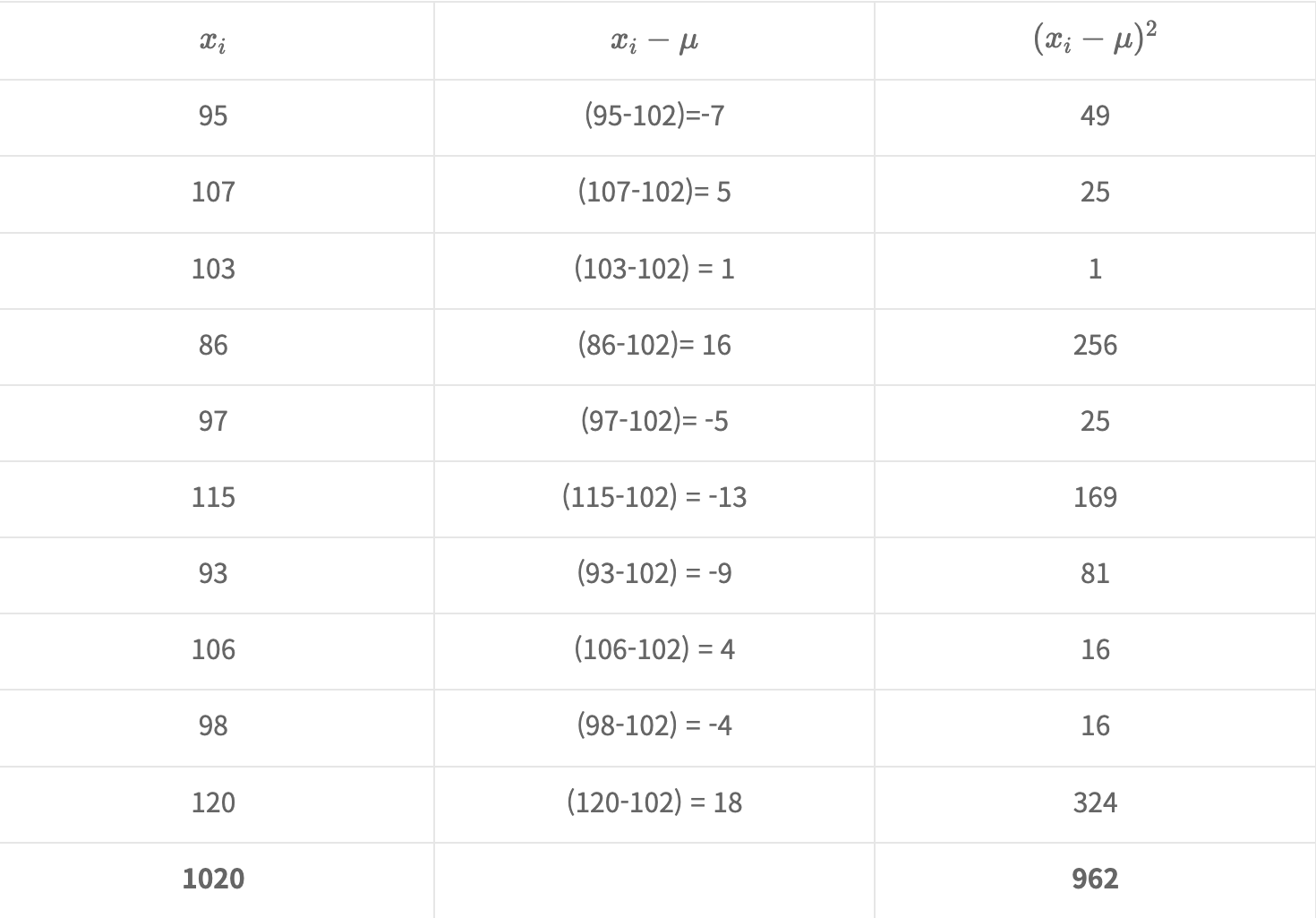
그러므로 분산은 $\sigma^2 = 962/10 = 96.2$, 표준 편차 $\sigma = \sqrt{96.2} = 9.81$ 입니다.
이 때, 명심해야할 것은 우리가 이 10명을 모집단으로 간주했다는 것인데요. 모집단의 분산과 표준편차를 구할 때와 표본집단(샘플)의 분산과 표준편차는 다르다는 것이 중요합니다.
표본집단(sample)의 분산 공식

아니, 왜 난데없이 n-1을 할까요 싶으신 분? 저는 처음에 표본 집단의 식을 마주했을 때, 뭐지 왜 일관성이 없지 하고 헷갈렸어서, 혹시 저와 같은 분들을 위해 설명해보도록 하겠습니다.
표본은 표본이 나온 모집단에 대한 통계적 추론을 만드는 데 사용됩니다.
모집단 데이터가 있으면 모집단 표준 편차에 대한 정확한 값을 얻을 수 있습니다. 모든 모집단 구성원으로부터 데이터를 수집하기 때문에 표준 편차는 모집단 분포의 정확한 변동성을 반영합니다. 그러나 표본 데이터를 사용할 때 표본 표준 편차는 항상 모집단 표준 편차의 추정치로 사용됩니다. 이 공식에서 표본의 수 n을 그대로 사용하면 변동성을 지속적으로 과소평가하는 편향된 추정치를 제공하는 경향이 있습니다.
심플하게 예를 들기 위해 모집단(population)에 (0,2,4) 가 있다고 가정합니다. 이 모집단의 평균 $\mu = 2$, 분산 $\sigma^2 = \frac{4+0+4}{3} = \frac{8}{3}$ 이 되겠죠. 이 중 2개를 셀렉하여 표본을 만드는데, replace와 순서까지 다 고려한 가능한 모든 리스트를 만들어봅니다.

위의 예에서 보았듯이, 샘플 n을 n – 1로 줄이면 표준 편차가 인위적으로 커져 변동성을 보수적으로 추정할 수 있습니다. 표본의 변동성을 과소 평가하는 것보다 과대 평가하는 것이 더 나은 이유는, 표본의 분산이 살짝 과대 평가 되었을 때 모분산에 더 가까워져, 표본을 통하여 모집단에 대한 정보 추론시 더 유용하기 때문입니다. 표준 편차의 편향된 추정치와 보수적인 추정치의 차이는 표본 크기가 클 때 훨씬 작아집니다. (표본 크기가 클 때에 모집단에 더 가까워진다는 사실과 일맥상통합니다.)
왜 표본분산 공식에서 n-1을 사용하는지, 간단하게 예시를 통해서 보여드렸는데요, 표본 표준편차에는 왜 n-1을 할까에서 수식을 통해 이해해보도록 하겠습니다.
'Stats101' 카테고리의 다른 글
| 표준오차, 표본오차와 신뢰구간 (1) | 2023.04.16 |
|---|---|
| 표본 표준편차에는 왜 n-1을 할까? (0) | 2023.04.12 |
| 귀무가설, 대립가설 그리고 P-hacking (0) | 2023.04.07 |
| m&m 초콜릿으로 P-value 쉽게 이해하기 (0) | 2023.04.06 |
| 표준화 및 표준 정규 분포(Standard Normal Distribution) (0) | 2023.04.04 |




댓글