지난 포스팅 분산과 표준편차에서 분산과 표준 편차 구하는 공식과 함께 어떻게 표본 집단의 분산에 n-1을 취했을 때 모분산과 같아지는지 예시를 통해서 설명하였습니다. 이번 포스팅에서는 수식을 통해서 이해해 보는 시간을 갖도록 해볼 거예요.
2023.04.09 - [Stats101] - 분산과 표준편차
분산과 표준편차
정규분포는 평균과 표준편차에 의해 분포의 모양이 결정됩니다. 여기서 표준편차는 분산의 제곱근으로 데이터의 변동성을 나타내는데요, 변동성이란 데이터가 서로 그리고 분포 중심(mu)에서
minitistics.tistory.com

일단 표본 집단과 표본 평균 집단이 다르다는 것을 알고 넘어가야 할 텐데요. 표본집단의 표준 편차를 계산할 때 왜 n-1인가를 설명하기 전에, 표본 평균 집단의 분산과 표준편차를 먼저 짚고 갈게요.
표본 평균 집단의 분산과 표준편차 (표본 집단 <> 표본 평균 집단)
모집단을 숫자 (1,3,5)이 들어있는 주머니로 가정하고, 이 중 2개의 숫자를 샘플로 뽑는 상황을 가정합니다. 이때 표본 평균 $\bar{X}$ 는 딱 2개의 숫자를 딱 한번 뽑았을 때의 평균을 말하는데요, 예를들어 1과 3을 뽑았다고 하면 우리의 표본 평균은 $\bar{X} = \dfrac{1+3}{2} = 2$ 가 됩니다. 아래의 식이 적용된 거죠.
$$\bar{X} = \dfrac{X_{1} + X_{2} + \cdots + X_{n}}{n}$$
자, 그럼 이제 우리가 도출할 수 있는 샘플 크기가 2가 되는 표본($n=2$)을 다 조합해 본 후, 각 표본의 평균을 구해보겠습니다.
| $X_{2}$ \ $X_{1}$ | 1 | 3 | 5 |
| 1 | 1 | 2 | 3 |
| 3 | 2 | 3 | 4 |
| 5 | 3 | 4 | 5 |
위의 표에 나온 각각의 표본 평균($\bar{X}$)이 일어날 확률을 나타내보면 다음과 같습니다.

표본 평균 집단의 평균은 $E(\bar{X})$로 나타내며, 이는 표본 평균(\bar{X})을 확률 변수로 사용하여 구한 평균입니다. 즉 평균의 평균을 구하는 것이죠.
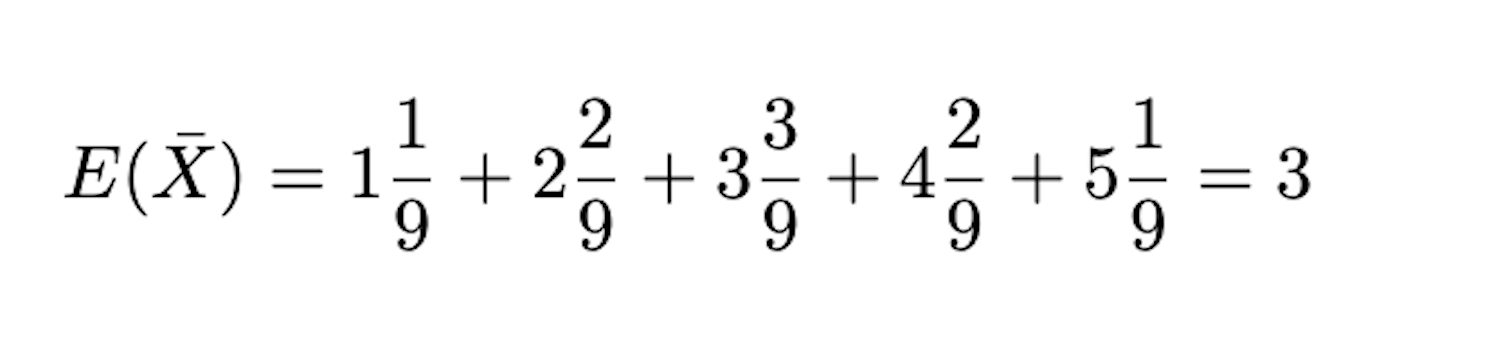
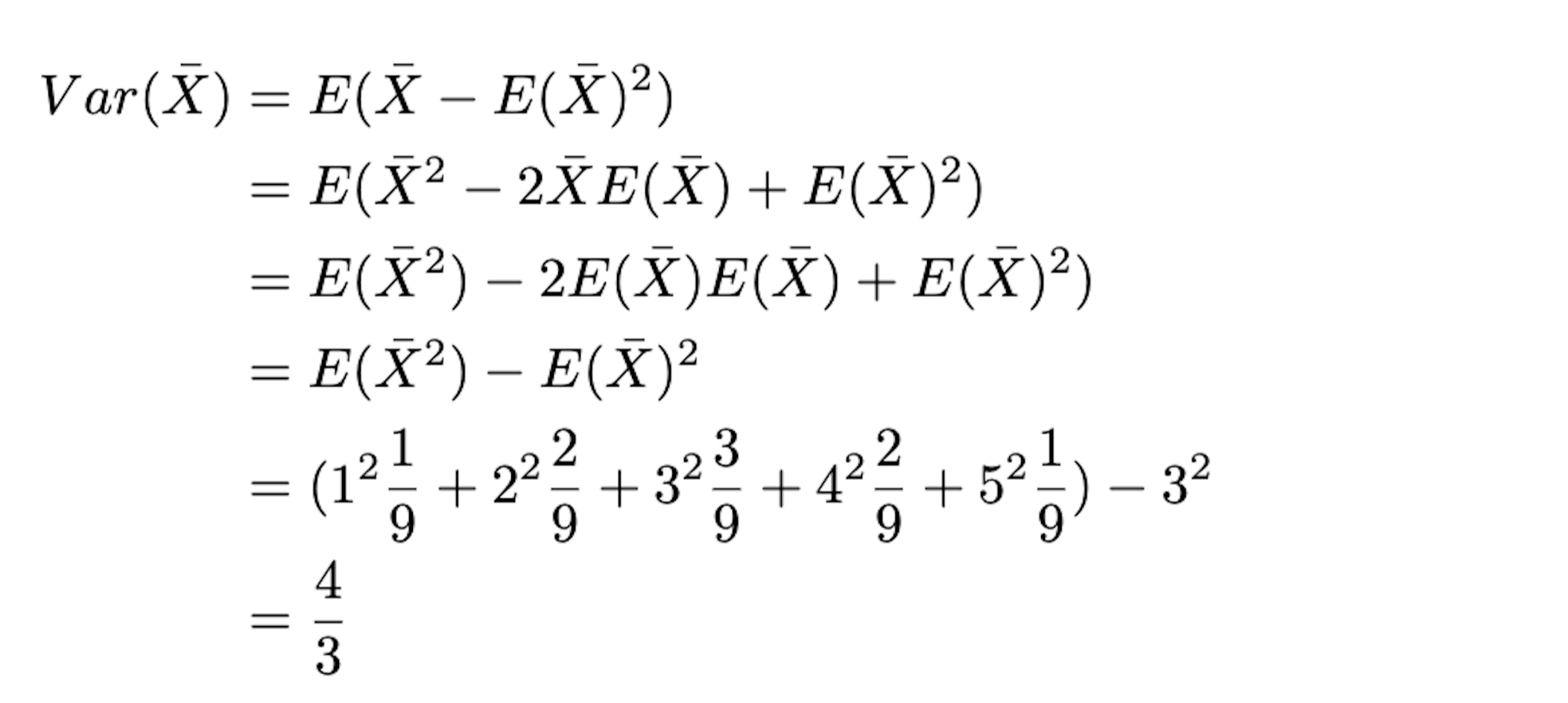
처음 주머니에 들었던 모집단의 숫자가 (1,3,5)였으니 이때 모평균($\mu$)은 3, 모분산($\sigma^2$)은 $\dfrac{8}{3}$ 이 됩니다. 그리고 우리가 계산한 표본 평균집단의 평균은 $E(\bar{X})= 3$ 로 모평균($\mu$)과 같고, 표본 평균집단의 분산($Var(\bar{X}) = \dfrac{4}{3}$) 은 모분산($\sigma^2$)에서 표본(샘플)의 수 2를 나눈 값($\dfrac{\sigma^2}{n}$)임을 알 수 있습니다.
이를 식으로 나타내어보면:
$X_{1}, X_{2}, X_{3}, \cdots, X_{n}$는 평균이 $\mu$이고 분산이 $\sigma^2$인 모집단에서 크기가 n인 무작위 표본이라고 정의합니다. 이때, 표본 평균집단의 평균, 즉 기댓값은:
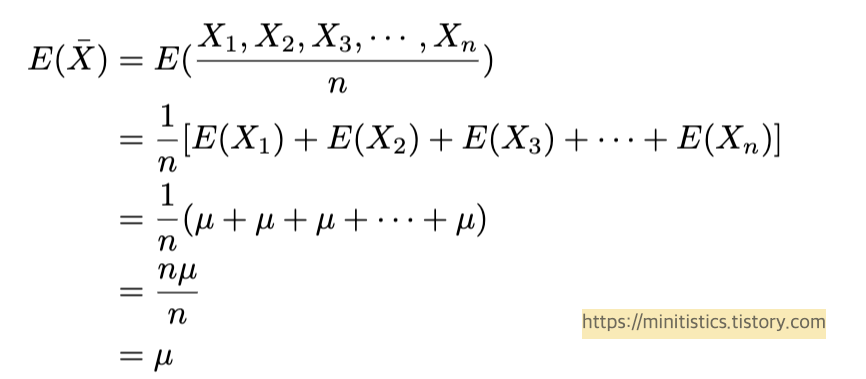
그리고 표본 평균집단의 분산은 다음과 같습니다.
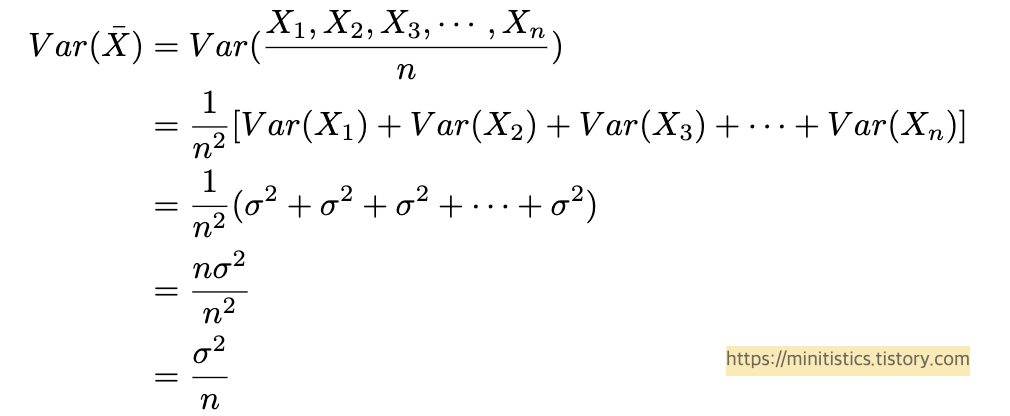
위의 식으로 보면 표본 크기가 증가함에 따라 표본 평균의 분산이 감소한다는 것을 알 수 있습니다. 이는 표본 수가 커질수록, 각 표본 평균의 변동성이 적다는 것을 의미합니다. 즉 3개 중에서 1개만 표본으로 할 때의 분산보다는, 2개(거의 모집단에 가까운 숫자)를 표본으로 하면, 각 샘플 집단 간의 변동성이 낮아진다는 뜻입니다.
여기까지 잘 따라오셨어요. 그럼 이제(이제야!), 본격적으로 표본의 표준편차에 왜 n-1을 하는지 알아보겠습니다.
모집단의 모든 데이터 포인트는 독립적이고 동일하게 분포되어 있다는 iid(Independent, identically distributied)를 가정합니다. 즉, 모든 관찰값이 동일한 모평균과 모분산을 갖게 됩니다.
증명을 시작하기 전에 일단 기억하고 가야 할 부분이 있습니다.
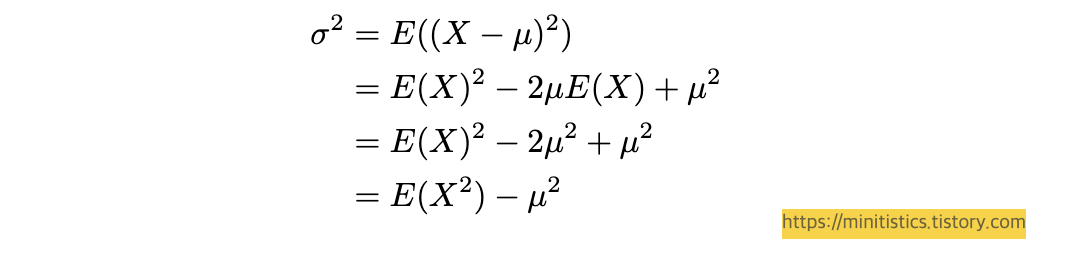
이는 다음과 같은 식을 도출하게 됩니다.
$$E(X^2) = \mu^2 + \sigma^2$$
제일 위의 표에서 설명되어 있듯, 표본 표준편차는 $s^2$으로 나타내고, 이 표준편차의 기댓값은 $E(s^2)$가 됩니다. 표본 분산에 대한 우리의 목표는 평균적으로 정확한 모집단 분산의 추정치를 제공하는 것입니다. 다른 샘플을 선택하면 $s^2$ 값이 달라지지만 많은 샘플을 선택하고 매번 $s^2$를 기록하면 해당 분포가 모분산인 $\sigma^2$에 집중되기를 기대합니다. $s^2$는 임의의 변수이므로(샘플마다 다른 값이 생성됨)$s^2$ 의 기댓값이 $\sigma^2$와 같아야 한다고 수학적으로 작성합니다.

따로 빼두었던 식을 대입하면,
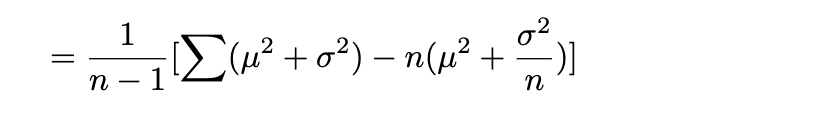
$E[X_{i}]$ 는 모든 $X_{i}$에 대하여 같은 값을 갖으므로 (iid)
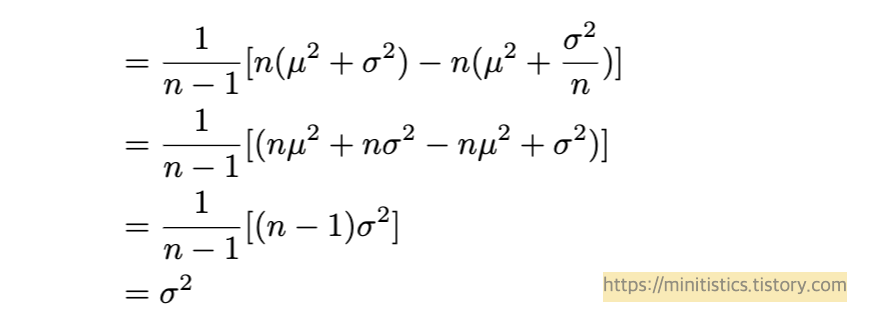
드디어 나왔죠!
$E(s^2) = \sigma^2$가 가능했던 건, 분모에 n이 아닌 n-1을 넣어서 가능했다는 걸 확인하였습니다.
왜 n-1을 할까를 설명하기 위해, 표본 평균 집단과 표본 집단의 다른 점, 표본 평균 집단의 평균과 분산을 구하는 법, 그리고 마침내 본격적인 증명까지 돌아 돌아서 여기까지 왔어요.
정말 수고하셨습니다!
'Stats101' 카테고리의 다른 글
| Confusion Matrix (0) | 2023.04.17 |
|---|---|
| 표준오차, 표본오차와 신뢰구간 (1) | 2023.04.16 |
| 분산과 표준편차 (0) | 2023.04.09 |
| 귀무가설, 대립가설 그리고 P-hacking (0) | 2023.04.07 |
| m&m 초콜릿으로 P-value 쉽게 이해하기 (0) | 2023.04.06 |




댓글