앞서 표본 표준편차에는 왜 n-1을 할까? 에서 표본 집단과 표본 평균집단이 다르다는 점을 설명하였는데요, 표준편차와 표본오차가 헷갈릴 수 있을 것 같아 잠시 짚고 넘어가보겠습니다.
2023.04.12 - [Stats101] - 표본 표준편차에는 왜 n-1을 할까?
표본 표준편차에는 왜 n-1을 할까?
지난 포스팅 분산과 표준편차에서 분산과 표준 편차 구하는 공식과 함께 어떻게 표본 집단의 분산에 n-1을 취했을 때 모분산과 같아지는지 예시를 통해서 설명하였습니다. 이번 포스팅에서는 수
minitistics.tistory.com
(1)표준편차(population standard deviation) : 모집단의 표준편차
(2)표본표준편차(sample standard deviation) : 표본의 표준편차
(3)표준오차(standard error) : 표본'평균'의 표준편차
(4)표본오차(margin of error or sampling error) : 임계값(alpha: critical value) * 표준오차
표본 집단은 숫자 (1,3,5)가 들어있는 주머니에서 딱 한 번 표본(샘플)으로 2개의 숫자를 뽑았을 때, 이를 표본 집단이라고 합니다. 그리고 이 과정을 여러번 반복하여 여러개의 샘플 집단이 만들어 각 샘플의 평균을 구했을 때, 그 집단을 표본 평균집단이라고 합니다.
표준편차(Standard Deviation)와 표준오차(Standard Error) 모두 데이터의 편차를 나타내는데, 표준편차는 한 샘플 내에서의 편차를 나타내고, 표준오차는(Standard Error)는 평균 집단간의 편차를 나타냅니다.
표준오차는 왜 중요할까?
표준오차는 모집단에서 뽑은 여러개의 표본(샘플)의 평균의 집단의 편차로, 표본 데이터가 전체 모집단을 얼마나 잘 대표하는지 추정할 수 있습니다. 무작위로 여러개의 표본을 뽑는 과정에서 표본이 모집단과 완전히 일치하지는 않기 때문에, 각각의 샘플 서로 다른 평균과 표준편차를 나타내게 되는데요, 이 표본집단의 평균간 편차가 표본 집단이 얼마나 모집단을 대표할 수 있는지를 안내해주는 역할을 합니다.
표준오차가 높으면 표본 평균이 모집단 평균 주위에 널리 퍼져 있음을 보여줍니다. 즉, 표본이 모집단을 거의 나타내지 않을 수 있습니다. 낮은 표본오차는 표본 평균이 모집단 평균 주위에 밀접하게 분포되어 있음을 나타냅니다. 즉, 표본이 모집단을 대표할 수 있다고 볼 수 있습니다.
표본 평균집단의 평균:

표본 평균집단의 분산:

표본 평균집단의 표준편차(=표준오차):

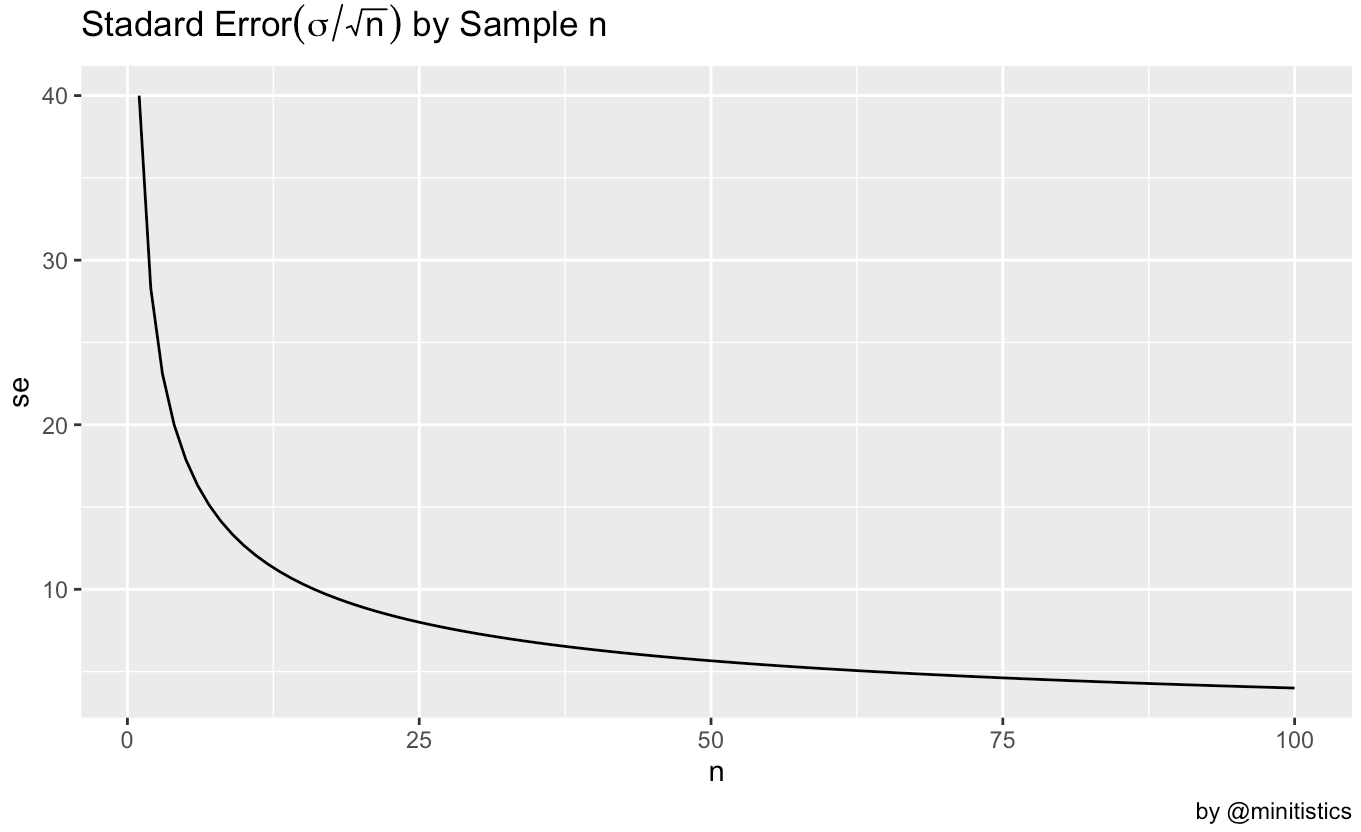
표본 크기를 늘려 표준오차를 줄일 수 있음을 알 수 있습니다. 당연하겠죠? 표본 수가 커질수록, 모집단의 수에 가깝기 때문에 변동성이 적다는 것을 의미합니다. 그러므로 표본의 편향을 최소하기 위해서는 사실 숫자가 큰 무작위 표본을 사용하는 것이 좋음을 알 수 있습니다.
다음은 표준편차($\sigma$)가 15일 때, 샘플(n)이 1 에서 100까지 증가했을 때, 표준오차의 변화를 그래프로 나타내었습니다.
표준오차, 표본오차와 신뢰구간
표준오차는 신뢰 구간과 관련이 있습니다. 표준화 및 표준 정규분포에서 설명했던 표준화 과정은 모집단 가정하에 예를 들어 우리는 데이터 포인트가 모평균($\mu$)에서 얼만큼의 편차($\sigma$)로 나타내었는데요:

통계의 궁극적 목적은 표본을 이용하여 모집단을 추정하는 것이기 때문에 여러 표본 집단을 이용하여 표본 평균 집단의 표준편차(표준오차)를 설명하려는 경우 Z-score는 다음과 같이 나타낼 수 있습니다. 이는 표본 평균 집단과 모집단 평균 사이에 얼마나 많은 표준 오차가 있는지 알려줍니다. (여기서 핵심은 표준 평균 집단의 분포를 다루고 있으므로 공식에 표준 오차를 포함해야 한다는 것!)

즉, 표본의 평균($\bar{X}$)이 모평균($\mu$)에서 얼만큼의 편차를 나타내는가이죠. 그리고 표본오차는 표준오차에서 임계값을 곱한 값이 됩니다.
여론 조사를 보면 보통 [표본오차는 95% 신뢰수준에서 $\pm$3%]와 같은 문구를 접하게 됩니다. 여기서 신뢰수준이 95%라는 뜻은 100번을 표본을 추출하였을 때, 1.95*표준오차(=표본오차, 여기선 3%) 범위 내에서 모평균이 있을 확률이 95%라는 뜻이 됩니다. 정규분포에서 정규분포의 해석을 다룰 때 모집단의 표준편차를 통해 모집단의 분포를 설명하면서, 이 과정이 통계의 본질인 표본(샘플)을 이용하여 모집단을 추론하는 과정에서 매우 유용하게 사용된다고 정리했는데 그 과정이 지금 여기 나오는거에요.
마치 정규분포에서, 학생 500명의 한 학교 학생들의 수학 시험 점수 평균을 75, 표준편차를 3으로 가정하고 95% 정도의 데이터포인트(각 학생의 점수)가 75-1.96*3, 75+1.96*3 사이에 존재한다고 했던 것과 같이, 여기서는 표본평균을 중심으로 표준오차만큼 어느 정도의 확신(95%)을 갖고 구간을 정하느냐가 됩니다. 그리고 그 값이 신뢰구간, 즉 Confidence Interval이에요.
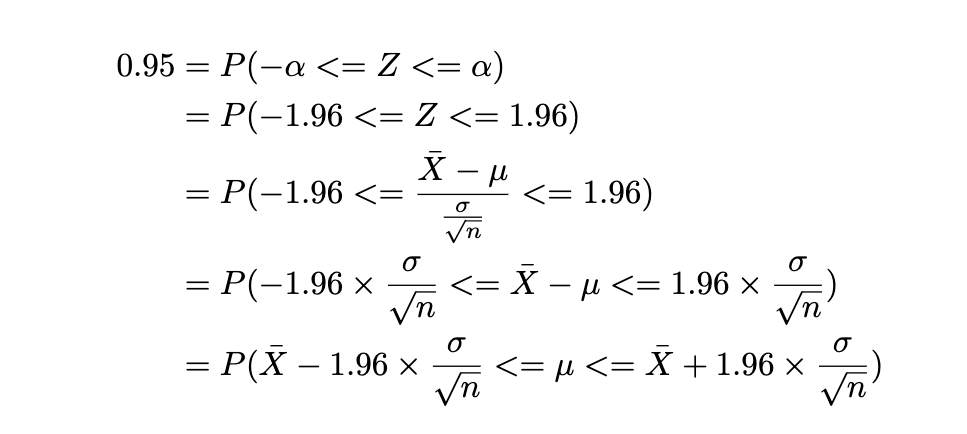
다음은 머니투데이 [60초 통계] 신뢰수준과 표본오차의 이해에서 나온 예시인데요, 여론조사에서 100명의 사람에게 질문한 결과 A 후보와 B 후보에 대한 지지율이 각각 40%, 36%가 나왔다고 하면, [표본오차는 95% 신뢰수준에서 $\pm$3%]라는 가정하에 따라 우리는 신뢰구간을 다음과 같이 정의할 수 있습니다.
- 95%의 확률로 모집단의 A후보에 대한 지지율이 37-43% 사이일 것이다.
- 95%의 확률로 모집단의 B후보에 대한 지지율이 33-39% 사이일 것이다.
눈치 채셨을 수도 있겠지만, 이 결과만 갖고 A후보가 승리할 확률이 높다라고 결론을 내릴 수 없습니다. 예를 들어, 95%의 확률로 모집단의 A에 대한 지지율이 37%, B 에 대한 지지율이 39%일 수도 있기 때문입니다.
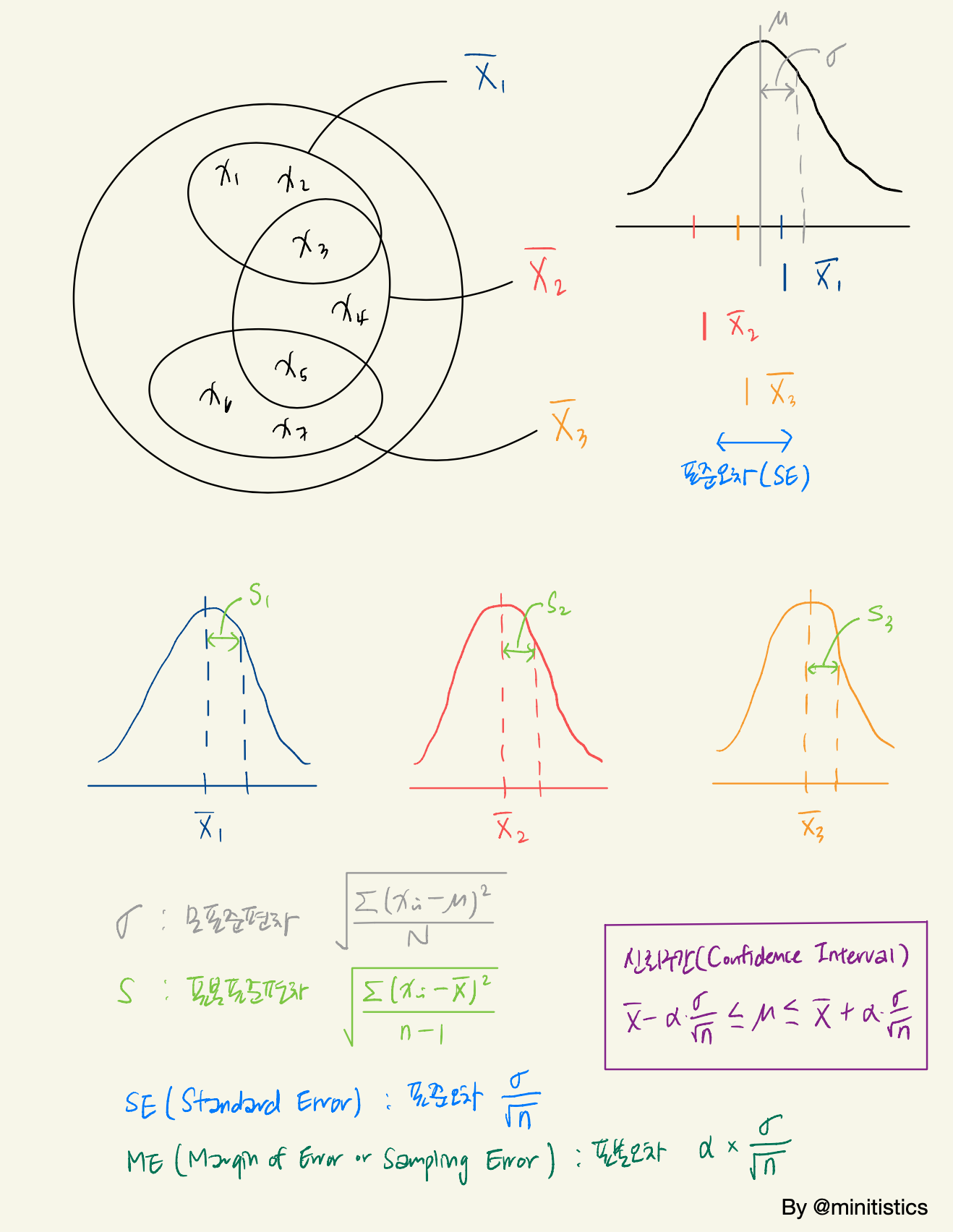
이상, 표준편차와 표준오차의 다른점, 그리고 표준오차를 이용하여 표본오차를 구한 후 신뢰구간을 계산하는 법까지 함께 배워봤습니다. 이 내용을 한 페이지로 정리해봤는데요, 아래를 참고해주세요 :)
'Stats101' 카테고리의 다른 글
| t-분포(t-Distribution) (0) | 2023.04.19 |
|---|---|
| Confusion Matrix (0) | 2023.04.17 |
| 표본 표준편차에는 왜 n-1을 할까? (0) | 2023.04.12 |
| 분산과 표준편차 (0) | 2023.04.09 |
| 귀무가설, 대립가설 그리고 P-hacking (0) | 2023.04.07 |




댓글