t-분포란?
t-분포 Student's t-distribution 이라고도 알려져있는데요, 모집단의 분산을 알 수 없는 더 작은 표본 크기에 사용되는 정규 분포 유형입니다. t분포를 그려보면 정규분포와 같이 종 모양을 형성하며, 평균 근처에 더 많은 관측치가 있고 꼬리부분이 두꺼운 것을 알 수 있어요(fat tail). 꼬리가 두껍다는 뜻은, 평균에서 먼 값, 즉 예상되는 값보다 훨씬 크거나 작은 값이 관찰될 확률이 높다는 뜻이 됩니다. 데이터 분포의 불확실성이 매우 크죠. t-분포가 작은 표본크기에 사용되는 분포이니만큼 예상된 결과라고 할 수 있습니다.
2023.04.01 - [Stats101] - 정규 분포(Normal Distribution)
정규 분포(Normal Distribution)
정규분포란? 정규분포(Normal Distribution)는 가우시안 분포(Gaussian Distribution)라고도 알려져 있는데요, 통계학에서의 검정이나 추정, 모델 작성 등 다양한 측면에서 활용되는 연속형 확률분포(Continuou
minitistics.tistory.com
t-분포를 사용하는 경우로는 주로 데이터가 대략적으로 정규 분포를 따른다는 가정 하에 신뢰 구간의 임계값을 찾거나, t-분포(t-test, 회귀 분석)를 사용하는 통계 테스트에서 해당 p-value를 찾습니다(마치 정규분포의 z-test(z-score)를 사용하듯이요). t-분포는 정규분포와 흡사하여 데이터가 종 모양을 따르지만 모집단 분산을 알 수 없습니다.
그럼 분산의 개념을 어떻게 도출할까요? 바로 자유도(Degree of Freedom = n-1)를 기준으로 추정됩니다.

도대체 얼마나 작은 표본이어야 할까?
자유도(df)가 증가함에 따라 t-분포는 표준 정규분포(z-분포)와 점점 더 가까워집니다. 앞서 t-분포를 표본이 작을 때 사용한다고 하였는데, 도대체 이 [작다]가 얼마나 작은 걸 말하는 걸까요?
다음은 자유도(Degree of Freedom, df)에 따라 달라지는 t-분포를 나타내보았습니다. 모분산을 모르는 대신 자유도를 통해 t-분포를 나타내는만큼, 자유도의 변화에 따라 t-분포도 달라짐을 알 수 있습니다.

위 그래프에서 비밀(?) 하나 찾아내신분?! 표준 정규분포도 함께 그려넣었는데요, 가만보면 자유도가 커질수록 t-분포가 정규분포에 근접해감을 알 수 있습니다.

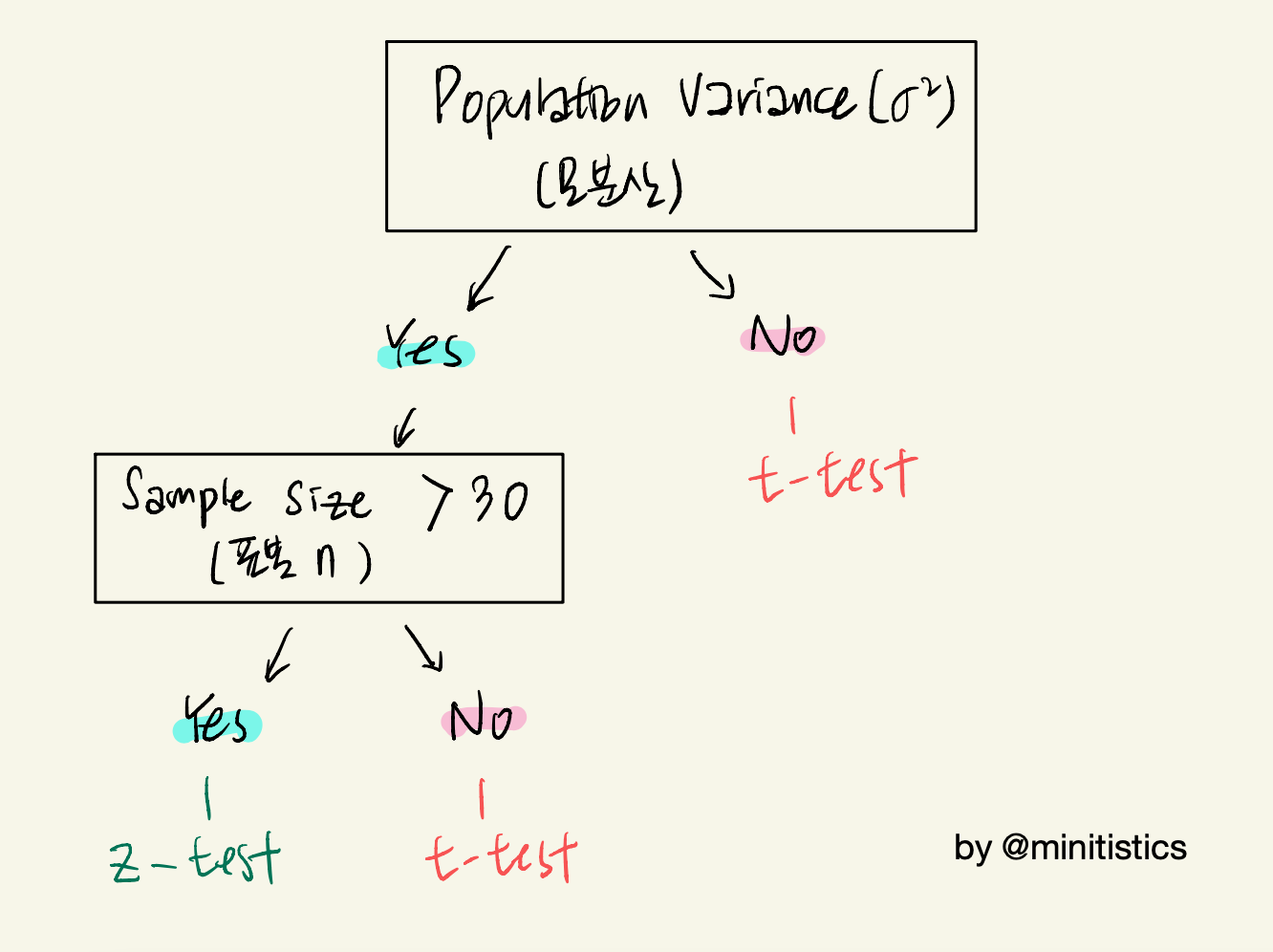
t-분포의 자유도가 30 이상일 때는 정규분포와 비슷합니다. 그래서 우리는 표본이 30 이상이고, 모분산을 알면 정규분포를 사용할 수 있어요. 정규분포는 우리가 이미 함께 공부했지만, 분산이 알려져 있기 때문에 통계적 추정을 할 때 t-분포보다 선호됩니다. 데이터의 자유도를 사용하여 분산의 근사값으로 사용하는 t-분포보다 더 정확한 추정을 할 수 있으니까요.
하지만 모분산을 알 수 있는 경우가 매우 드물기 때문에, t-test도 많이 사용하는 통계검정 중 하나입니다. 그럼 t검정을 위한 t-score는 어떻게 구하는지 알아보겠습니다.
t-score 구하는 법
모분산(혹은 모집단의 표준편차)를 모르고 작은 표본(30 미만)이 있는 경우 t-score 공식을 사용하는 것이 좋습니다.
t 점수 공식은 다음과 같습니다.

ˉX= 표본 평균
μ = 모집단 평균
s = 표본 표준편차
n = 표본 크기
그런데 이 식, 어디서 본 것 같지 않나요?
2023.04.04 - [Stats101] - 표준화 및 표준 정규 분포(Standard Normal Distribution)
표준화 및 표준 정규 분포(Standard Normal Distribution)
정규분포(Normal Distribution)에서 잠시 언급하였듯, 정규 분포를 따르는 자연 현상이나 사회 현상은 무궁무진합니다. 그만큼 정규분포를 구성하는 평균과 분산이 다양하기 때문에, 세상의 모든 정
minitistics.tistory.com
z-score 와 잠시 비교하고 가자면:
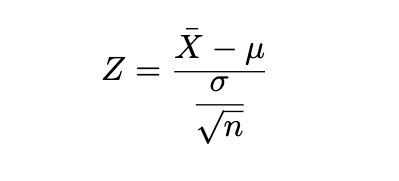
표준의 크기가 크고 모분산을 알고 있을 때 Z-score 를 사용할 수 있으니, z-score 의 모분산과 t-score의 표준분산이 대체됨을 알 수 있습니다. 계속 반복되는 개념이라 지겨워도 그만큼 머리속에 쏙쏙 자리를 잡아가길 바라며, 미니노트 남겨봅니다.
t-score 는 언제 어떻게 사용할까?
t-score는 가설검정 t-test를 할 때 사용하는데요. 3가지 테스트가 있습니다:
- 단일표본 t-test (one-sample t-test): 단일 평균에 대한 가설 검정
- 독립표본 t-test (two-sample t-test): 서로 다른 두 집단의 평균 차이에 대한 가설 검정
- 대응표본 t-test (paired t-test): 동일 집단에서 변화를 나타내는 평균의 차이에 대한 가설 검정
위의 가설 검정에 대해서는 조만간 포스팅하도록 하겠습니다. 오늘은 t-분포가 무엇이다!를 정확히 이해하는 것만으로도 나 자신 잘했어, 수고했어 해봅니다 :)
'호주 데이터 분석가 > Stats101' 카테고리의 다른 글
| 일원 분산분석 (One-way ANOVA) (0) | 2023.04.23 |
|---|---|
| t 검정의 종류와 방법 (0) | 2023.04.21 |
| Confusion Matrix (0) | 2023.04.17 |
| 표준오차, 표본오차와 신뢰구간 (1) | 2023.04.16 |
| 표본 표준편차에는 왜 n-1을 할까? (0) | 2023.04.12 |




댓글